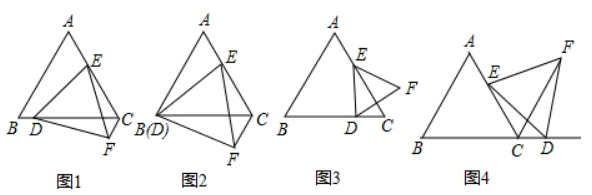
如图1, $\triangle A B C$ 是等边三角形, 点 $E$ 在 $A C$ 边上, 点 $D$ 是 $B C$ 边上的一个动点, 以 $D E$ 为边作等边 $\triangle D E F$, 连接 $C F$.
(1) 当点 $D$ 与点 $B$ 重合时, 如图 2 , 求证: $C E+C F=C D$;
(2) 当点 $D$ 运动到如图 3 的位置时, 猜想 $C E 、 C F 、 C D$ 之间的等量关系, 并说明理由;
(3) 只将条件 “点 $D$ 是 $B C$ 边上的一个动点” 改为 “点 $D$ 是 $B C$ 延长线上的一个动点”, 如图 4 , 猜想 $C E 、 C F 、 C D$ 之间的等量关系为 (不必证明)。
(1) 当点 $D$ 与点 $B$ 重合时, 如图 2 , 求证: $C E+C F=C D$;
(2) 当点 $D$ 运动到如图 3 的位置时, 猜想 $C E 、 C F 、 C D$ 之间的等量关系, 并说明理由;
(3) 只将条件 “点 $D$ 是 $B C$ 边上的一个动点” 改为 “点 $D$ 是 $B C$ 延长线上的一个动点”, 如图 4 , 猜想 $C E 、 C F 、 C D$ 之间的等量关系为 (不必证明)。
