单选题 (共 9 题 ),每题只有一个选项正确
"狼来了"的故事大家小时候应该都听说过:小孩第一次喊"狼来了",大家信了,但去了之后发现没有狼;第二次喊"狼来了",大家又信了,但去了之后又发现没有狼;第三次狼真的来了,但是这个小孩再喊狼来了就没人信了.从数学的角度解释这一变化,假设小孩是诚实的,则他出于某种特殊的原因说谎的概率为 0.1 ;小孩是不诚实的,则他说谎的概率是 0.5 .最初人们不知道这个小孩诚实与否,所以在大家心目中每个小孩是诚实的概率是 0.9 .已知第一次他说谎了,那么他是诚实的小孩的概率是( )
$\text{A.}$ $\frac{3}{5}$
$\text{B.}$ $\frac{5}{7}$
$\text{C.}$ $\frac{7}{10}$
$\text{D.}$ $\frac{9}{14}$
甲口袋中有 3 个红球, 2 个白球和 5 个黑球,乙口袋中有 3 个红球, 3 个白球和 4 个黑球,先从甲口袋中随机取出一球放入乙口袋,分别以 $A_1, A_2$ 和 $A_3$ 表示由甲口袋取出的球是红球,白球和黑球的事件;再从乙口袋中随机取出一球,以 $B$ 表示由乙口袋取出的球是红球的事件,则下列结论中正确的是
$\text{A.}$ $P\left(B \mid A_2\right)=\frac{4}{11}$
$\text{B.}$ 事件 $A_1$ 与事件 $B$ 相互独立
$\text{C.}$ $P\left(A_3 \mid B\right)=\frac{1}{2}$
$\text{D.}$ $P(B)=\frac{3}{10}$
设某公路上经过的货车与客车的数量之比为 $2: 1$ ,货车中途停车修理的概率为 0.02 ,客车为 0.01 ,今有一辆汽车中途停车修理,则该汽车是货车的概率为( )
$\text{A.}$ 0.8
$\text{B.}$ 0.6
$\text{C.}$ 0.5
$\text{D.}$ 0.3
某校对高三男生进行体能抽测,每人测试三个项目, 1000 米为必测项目,再从"引体向上,仰卧起坐,立定跳远"中随机抽取两项进行测试,则某班参加测试的 5 位男生测试项目恰好相同的概率为( )
$\text{A.}$ $\frac{1}{243}$
$\text{B.}$ $\frac{1}{81}$
$\text{C.}$ $\frac{1}{27}$
$\text{D.}$ $\frac{1}{9}$
在数字通信中,信号是由数字 0 和 1 组成.由于随机因素的干扰,发送的信号 0 或 1 有可能被错误地接收为 1 或 0 。已知发信号 0 时,接收为 0 和 1 的概率分别为 0.9 和 0.1 ;发送信号 1 时,接收为 1 和 0 的概率分别为 0.95 和 0.05 ,若发送信号 0 和 1 是等可能的,则接受信号为 1 的概率为( )
$\text{A.}$ 0.475
$\text{B.}$ 0.525
$\text{C.}$ 0.425
$\text{D.}$ 0.575
一个不透明的袋中装有 4 个红球, 4 个黑球, 2 个白球,这些球除颜色外,其他完全相同,现从袋中一次性随机抽取 3 个球,事件 $A$ :"这 3 个球的颜色各不相同",事件 $B$ :"这 3 个球中至少有 1 个黑球",则 $P(A \mid B)=$
$\text{A.}$ $\frac{5}{9}$
$\text{B.}$ $\frac{4}{9}$
$\text{C.}$ $\frac{17}{25}$
$\text{D.}$ $\frac{8}{25}$
现有甲、乙、丙三个工厂加工的同种产品各 100 件,按标准分为一、二两个等级、其中甲、乙、丙三个工厂的一等品各有 60 件、 70 件、 80 件.从这 300 件产品中任选一件产品,则下列说法错误的是
$\text{A.}$ 选中的产品是甲厂的一等品与选中的产品是乙厂的二等品互斥
$\text{B.}$ 选中的产品是一等品的概率为 $\frac{7}{10}$
$\text{C.}$ 选中的产品是丙厂生产的二等品的概率为 $\frac{1}{15}$
$\text{D.}$ 选中的产品是丙厂生产的产品与选中的产品是二等品相互独立
某人周一至周五每天 6: 30 至 6: 50 出发去上班,其中在 6:30 至 6:40 出发的概率为 0.4 ,在该时间段出发上班迟到的概率为 0.1 ;在 6:40至 6:50出发的概率为 0.6 ,在该时间段出发上班迟到的概率为 0.2 ,则小王某天在 $6: 30$ 至 $6: 50$ 出发上班迟到的概率为
$\text{A.}$ 0.3
$\text{B.}$ 0.17
$\text{C.}$ 0.16
$\text{D.}$ 0.13
根据历年的气象数据,某市 5 月份发生中度雾霸的概率为 0.25 ,刮四级以上大风的概率为 0.4 ,既发生中度雾霸又刮四级以上大风的概率为 0.2 ,则在刮四级以上大风的情况下,发生中度雾䨳的概率为
$\text{A.}$ 0.5
$\text{B.}$ 0.625
$\text{C.}$ 0.8
$\text{D.}$ 0.9
多选题 (共 2 题 ),每题有多个选项正确
甲箱中有 5 个红球, 2 个白球和 3 个黑球,乙箱中有 4 个红球, 3 个白球和 3 个黑球。先从甲箱中随机取出一球放入乙箱,分别以 $A_1, A_2$ 和 $A_3$ 表示由甲箱取出的球是红球,白球和黑球的事件;再从乙箱中随机取出一球,以 $B$ 表示由乙箱取出的球是红球的事件,则下列结论正确的是
$\text{A.}$ 事件 $B$ 与事件 $A_i(i=1,2,3)$ 相互独立
$\text{B.}$ $P\left(A_1 B\right)=\frac{5}{22}$
$\text{C.}$ $P(B)=\frac{2}{5}$
$\text{D.}$ $P\left(A_2 \mid B\right)=\frac{8}{45}$
已知编号为 $1,2,3$ 的三个盒子,其中 1 号盒子内装有两个 1 号球,一个 2 号球和一个 3 号球; 2 号盒子内装有两个 1 号球,一个 3 号球; 3 号盒子内装有三个 1 号球,两个 2 号球。若第一次先从 1 号盒子内随机抽取 1 个球,将取出的球放入与球同编号的盒子中,第二次从该盒子中任取一个球,则下列说法正确的是()
$\text{A.}$ 在第一次抽到 2 号球的条件下,第二次抽到 1 号球的概率为 $\frac{1}{2}$
$\text{B.}$ 第二次抽到 3 号球的概率为 $\frac{11}{48}$
$\text{C.}$ 如果第二次抽到的是 1 号球,则它来自 2 号盒子的概率最大
$\text{D.}$ 如果将 5 个不同的小球放入这三个盒子内,每个盒子至少放 1 个,则不同的放法有 300 种
填空题 (共 5 题 ),请把答案直接填写在答题纸上
有 3 台车床加工同一型号的零件,第 1 台加工的次品率为 $8 \%$ ,第 2 台加工的次品率为 $3 \%$ ,第 3 台加工的次品率为 $2 \%$ ,加工出来的零件混放在一起.已知第 $1,2,3$ 台车床加工的零件数分别占总数的 $10 \%, 40 \%$ , $50 \%$ ,从混放的零件中任取一个零件,如果该零件是次品,那么它是第 3 台车床加工出来的概率为
学校给每位教师随机发了一箱苹果,李老师将其分为两份,第 1 份占总数的 $40 \%$ ,次品率为 $5 \%$ ,第 2 份占总数的 $60 \%$ ,次品率为 $4 \%$ .若李老师分份之前随机拿了一个发现是次品后放回,则该苹果被分到第 1份中的概率为
某考生回答一道有 4 个选项的选择题,设会答该题的概率是 $\frac{3}{5}$ ,并且会答时一定能答对,若不会答,则在 4个答案中任选 1 个.已知该考生回答正确,则他确实会答该题的概率是
某学习小组共有 11 名成员,其中有 6 名女生,为了解学生的学习状态,随机从这 11 名成员中抽选 2 名任小组组长,协助老师了解情况, A 表示"抽到的 2 名成员都是女生",$B$ 表示"抽到的 2 名成员性别相同",则 $P(A \mid B)=$
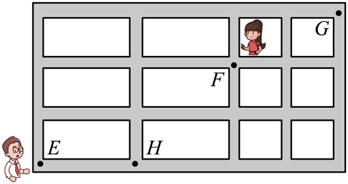
"五一"假期期间,小明和小红两位同学计划去四川省图书馆与老师探讨作业试卷上的圆锥曲线大题.如图,小红在街道 $E$ 处,小明在街道 $F$ 处,四川省图书馆位于 $G$ 处.二人均选择最短路线并约定在天府广场汇合,记事件 A :小红经过 $F$ ,事件 $B$ :小红经过 $H$ ,则 $P(A \mid B)=$
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
某批规格相同的产品由甲、乙、丙三个工厂共同生产,甲厂生产的产品次品率为 $2 \%$ ,乙厂和丙厂生产的产品次品率均为 $4 \%$ ,三个工厂生产的产品混放在一起,已知甲、乙、丙三个工厂生产的产品数分别占总数的 $40 \%, 40 \%, 20 \%$ .
(1)任选一件产品,计算它是次品的概率;
(2)如果取到的产品是次品,分别计算此次品出自甲厂、乙厂和丙厂的概率.
甲、乙两人进行乒乓球比赛,已知每局比赛甲获胜的概率为 $\frac{2}{3}$ ,乙获胜的概率为 $\frac{1}{3}$ ,且各局比赛的胜负互不影响。有两种比赛方案供选择,方案一:三局两胜制(先胜 2 局者获胜,比赛结束);方案二:五局三胜制 (先胜 3 局者获胜,比赛结束)。
(1)若选择方案一,求甲获胜的概率;
(2)用抛掷骰子的方式决定比赛方案,抛掷两枚质地均匀的骰子,观察两枚骰子向上的点数,若"两枚骰子向上的点数之和不大于 $6^{\prime \prime}$ 则选择方案一;否则选择方案二.判断哪种方案被选择的可能性更大,并说明理由.