填空题 (共 3 题 ),请把答案直接填写在答题纸上
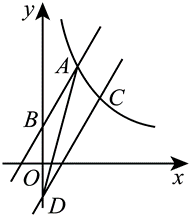
如图,已知直线 $y=k x(k>0)$ 分别交反比例函数 $y=\frac{1}{x}$ 和 $y=\frac{4}{x}$ 在第一象限的图象于点 $A$ , $B$ ,过点 $B$ 作 $B D \perp x$ 轴于点 $D$ ,交 $y=\frac{1}{x}$ 的图象于点 $C$ ,连接 $A C$ .若 $ A B C$ 是等腰三角形,则 $k$ 的值是
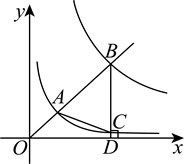
如图,矩形 $O A B C$ 位于直角坐标系中,点 $B(6 k, 3 k)$ 在第一象限内,点 $A$ 在 $x$ 轴上,点 $C$ 在 $y$ 轴上,反比例函数 $y=\frac{k+1}{x}$ 的图象交 $A B$ 于点 $F$ ,交 $B C$ 于点 $E$ ,点 $D$ 在边 $O A$ 上.若 $\triangle D E F$ 恰好是以 $E F$ 为斜边的等腰直角三角形,则 $k$ 的值为
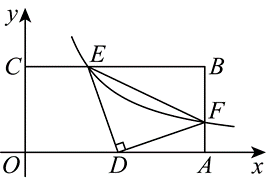
3.如图,点 $A$ 是反比例函数 $y=\frac{6}{x}(x>0)$ 的图象上一点,过点 $A$ 作直线 $y=-x$ 的垂线,垂足为点 $B$ ,再过点 $A$ 作 $A C \perp A B$ 交 $y=\frac{6}{x}(x>0)$ 的图象于点 $C$ ,若 $\triangle A B C$ 是等腰三角形,则点 $B$ 的坐标是 $\_\_\_\_$ .
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
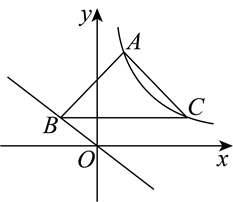
如图所示,一次函数 $y=x+3$ 的图象与反比例函数 $y=\frac{k}{x}$ 的图象交于 $A, B$ 两点,与 $x$ 轴、 $y$ 轴分别交于 $C, D$ 两点,连接 $O B, S_{\triangle B O D}=3$ .
(1)求 $k$ 的值.
(2)$x$ 轴上是否存在一点 $E$ ,使 $\triangle A B E$ 为等腰三角形?若存在,求出点 $E$ 的坐标;若不存在,请说明理由.
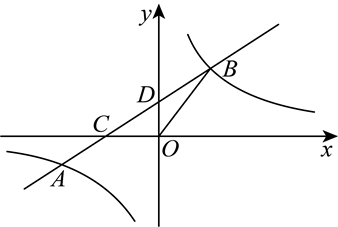
如图,反比例函数 $y=\frac{m}{x}$ 的图象与一次函数 $y=k x+b$ 的图象交于点 $A(-2,1)$ 和 $B(-1, n)$
(1)分别求出反比例函数与一次函数的解析式;
(2)根据图象直接写出不等式 $\frac{m}{x}>k x+b$ 的解集;
(3)在 $x$ 轴上是否存在点 $P$ 使 $\triangle O A P$ 为等腰三角形,若存在,直接写出所有符合条件的点 $P$的坐标;若不存在,请说明理由.
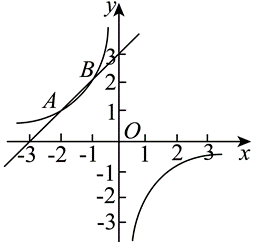
6.如图,直线 $y=k x+b$ 与 $x$ 轴交于点 $A(4,0)$ ,与 $y$ 轴交于点 $B(0,-2)$ ,与反比例函数 $y= \frac{k}{x}(x>0)$ 的图象交于点 $C(m, 1)$ .
(1)求直线和反比例函数的表达式.
(2)结合图象,请直接写出不等式 $\frac{k}{x} \geq a x+b$ 的解集.
(3)连接 $O C$ ,在 $x$ 轴上找一点 $P$ ,使 $\triangle O P C$ 是以 $O C$ 为腰的等腰三角形,请求出点 $P$ 的坐标.
如图,反比例函数 $y_1=\frac{m}{x}$ 图象与正比例函数 $y_2=n x$ 图象相交于点 $A(-1,2)$ 与点 $B$ .
(1)试求反比例函数 $y_1=\frac{m}{x}$ 与正比例函数 $y_2=n x$ 的函数表达式及点 $B$ 的坐标.
(2)请直接写出 $\frac{m}{x}>n x$ 的解集。
(3)现把 $y_2=n x$ 的图象绕 $O$ 点顺时针旋转 $90^{\circ}$ 得到了 $y_3=a x$ .试问在 $y_3=a x$ 函数图象上是否存在一动点 $E$ ,使 $\triangle A B E$ 是以 $B E$ 为底边的等腰三角形?如果有,请求出这个点 $E$ 的坐标;如果没有,请说明理由.
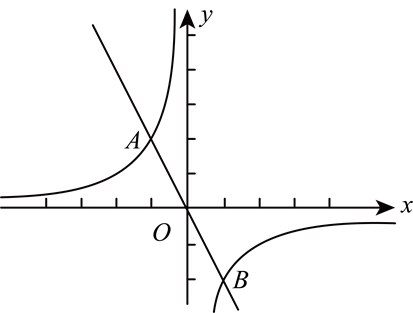
如图,已知反比例函数 $y=\frac{k}{2 x}$ 和一次函数 $y=2 x-1$ ,其中一次函数的图象经过 $(a, b)$ , $(a+1, b+k)$ 两点.
(1)求反比例函数的解析式;
(2)如下图,已知点 $A$ 在第一象限,且同时在上述两个函数的图象上,求点 $A$ 的坐标;
(3)利用(2)的结果为条件,请问:在 $x$ 轴上是否存在点 $P$ ,使 $\triangle A O P$ 是以 $A O$ 为腰的等腰三角形?若存在,直接写出点 $P$ 的坐标.
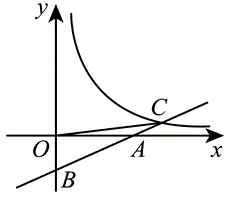
如图,一次函数 $y=\frac{4}{3} x+\frac{2}{3}$ 的图象与反比例函数 $y=\frac{k}{x}(x>0)$ 的图象交于点 $A(a, 2)$ ,与 $x$ 轴交于点 $B$ ,与 $y$ 轴交于点 $C$ ,连接 $A O$ .
(1)求反比例函数的表达式及点 $B$ 的坐标;
(2)将直线 $A B$ 向下平移 $m(m>0)$ 个单位长度得到直线 $l: y=\frac{4}{3} x+\frac{2}{3}-m$ ,设直线 $l$ 与反比例函数 $y=\frac{k}{x}(x>0)$ 的图象交于点 $P$ ,与 $x$ 轴交于点 $D$ .
① 连接 $A P, B P$ ,若 $S_{\triangle A B P}=3 S_{\triangle A O C}$ ,求 $m$ 的值;
② 连接 $A D, C D$ ,当 $\triangle A C D$ 是等腰三角形时,请直接写出点 $D$ 到直线 $A B$ 的距离.
如图,$y=\frac{k}{x}(x>0)$ 与次函数 $y=m x+2$ 的图像交于点 $A(2,6), y=m x+2$ 的图像交 $y$轴于点 $B$ .将过点 $A 、 B$ 的直线向下平移,平移后的直线与反比例函数的图像交于点 $C$ ,交 $y$ 轴于点 $D$ ,且点 $C$ 的横坐标为 3 .
(1)求 $k, m$ 的值;
(2)直接写出当 $x>0$ 时,不等式 $\frac{k}{x}>m x+2$ 的解集: $\_\_\_\_$ ;
(3)在 $x$ 轴负半轴上确定一点 $E$ ,使得以 $A 、 D 、 E$ 三点为顶点的三角形是等腰三角形,请求出所有符合条件的点 $E$ 的坐标.