单选题 (共 10 题 ),每题只有一个选项正确
设 $F_{1}, F_{2}$ 为椭圆 $C: \frac{x^{2}}{5}+y^{2}=1$ 的两个焦点,点 $P$ 在 $C$ 上,若 $\overrightarrow{P F_1} \cdot \overrightarrow{P F_2}=0$ ,则 $\left|P F_1\right| \cdot\left|P F_2\right|=(\quad)$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 4
$\text{D.}$ 5
已知 $O$ 是平面上的一定点,$A, B, C$ 是平面上不共线的三个动点,若动点 $P$ 满足 $\overrightarrow{O P}=\overrightarrow{O A}+\lambda(\overrightarrow{A B}+\overrightarrow{A C})$ , $\lambda \in(0,+\infty)$ ,则点 $P$ 的轨迹一定通过 $\triangle A B C$ 的
$\text{A.}$
$\text{B.}$ 内心
$\text{C.}$ 外心
$\text{D.}$ 重心
$\text{E.}$ 垂心
在 $\triangle \mathrm{ABC}$ 中,$(\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{BA}}) \cdot \overrightarrow{\mathrm{AC}}=|\overrightarrow{\mathrm{AC}}|^{2}$ ,则 $\triangle \mathrm{ABC}$ 的形状一定是 $\qquad$三角形.
$\text{A.}$ 等边
$\text{B.}$ 等腰
$\text{C.}$ 直角
$\text{D.}$ 等腰直角
若 $O$ 为 $\triangle A B C$ 所在平面内的任意一点,且满足 $(\overrightarrow{O B}-\overrightarrow{O C}) \cdot(\overrightarrow{O B}+\overrightarrow{O C}-2 \overrightarrow{O A})=0$ ,则 $\triangle A B C$ 的形状为( )
$\text{A.}$
$\text{B.}$ 等腰三角形
$\text{C.}$ 直角三角形
$\text{D.}$ 等边三角形
$\text{E.}$ 等腰直角三角形
已知菱形 $ A B C D$ 的边长为 $6, \angle A B D=30^{\circ}$ ,点 $E, F$ 分别在边 $B C, D C$ 上,且 $B C=2 B E, C D=\lambda C F$ .若 $\overrightarrow{A E} \cdot \overrightarrow{B F}=-9$ ,则 $\lambda$ 的值为( )
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
等腰直角三角形 $ A B C$ 中,$\angle A C B=\frac{\pi}{2}, A C=B C=2$ ,点 $P$ 是斜边 $A B$ 上一点,且 $B P=2 P A$ ,那么 $\overrightarrow{C P} \cdot \overrightarrow{C A}+$ $\overrightarrow{C P} \cdot \overrightarrow{C B}=(\quad)$
$\text{A.}$
$\text{B.}$ -4
$\text{C.}$ -2
$\text{D.}$ 2
$\text{E.}$ 4
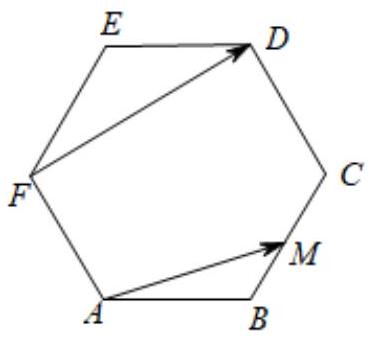
如图,正六边形 $ A B C D E F$ 的边长为 2 ,动点 $M$ 从顶点 $B$ 出发,沿正六边形的边逆时针运动到顶点 $F$ ,若 $\overrightarrow{F D} \cdot \overrightarrow{A M}$的最大值和最小值分别是 $m, n$ ,则 $m+n=()$
$\text{A.}$
$\text{B.}$ 9
$\text{C.}$ 10
$\text{D.}$ 11
$\text{E.}$ 12
在 $\triangle A B C$ 中,$A=\frac{\pi}{3}, G$ 为 $\triangle A B C$ 的重心,若 $\overrightarrow{A G} \cdot \overrightarrow{A B}=\overrightarrow{A G} \cdot \overrightarrow{A C}=6$ ,则 $\triangle A B C$ 外接圆的半径为
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $\frac{4 \sqrt{3}}{3}$
$\text{C.}$ 2
$\text{D.}$ $2 \sqrt{3}$
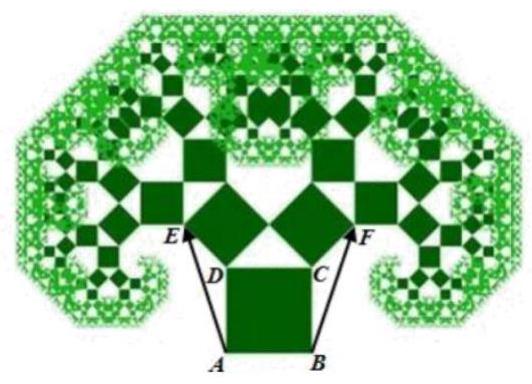
如图所示是毕达哥拉斯的生长程序:正方形上连接着等腰直角三角形,等腰直角三角形边上再连接正方形,如此继续,设初始正方形 $ A B C D$ 的边长为 $\sqrt{2}$ ,则 $AE \cdot BF=$
$\text{A.}$
$\text{B.}$ 2
$\text{C.}$ 4
$\text{D.}$ 6
$\text{E.}$ 8
已知点 $P$ 在圆 $x^{2}+y^{2}=1$ 上,点 $A$ 的坐标为 $(-2,-1), O$ 为坐标原点,则 $\overrightarrow{A O} \cdot \overrightarrow{A P}$ 的最小值等于( )
$\text{A.}$ 3
$\text{B.}$ $5-\sqrt{5}$
$\text{C.}$ 4
$\text{D.}$ $5+\sqrt{5}$
多选题 (共 2 题 ),每题有多个选项正确
已知点 $O$ 是边长为 1 的正方形 $ A B C D$ 的中心,则下列结论正确的为( )
$\text{A.}$ $\overrightarrow{A O}=\frac{1}{2}(\overrightarrow{A B}+\overrightarrow{A D})$
$\text{B.}$ $\overrightarrow{A B} \cdot \overrightarrow{B O}>0$
$\text{C.}$ $\overrightarrow{A O}=\overrightarrow{B O}$
$\text{D.}$ $|2 \overrightarrow{A B}-\overrightarrow{A D}|=\sqrt{5}$
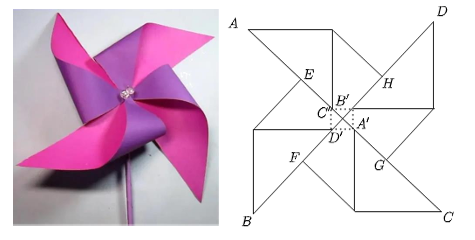
折纸发源于中国.19世纪,折纸传入欧洲,与自然科学结合在一起成为建筑学院的教具,并发展成为现代几何学的一个分支.我国传统的一种手工折纸风车(如图1)是从正方形纸片的一个直角顶点开始,沿对角线部分剪开成两个角,将其中一个角折叠使其顶点仍落在该对角线上,同样操作其余三个直角制作而成的,其平面图如图2,则( )
$\text{A.}$ $\overrightarrow{E H} / / \overrightarrow{F C}$
$\text{B.}$ $\overrightarrow{A H} \cdot \overrightarrow{B E}=0$
$\text{C.}$ $\overrightarrow{E G}=\overrightarrow{E H}+\overrightarrow{E F}$
$\text{D.}$ $\overrightarrow{E C} \cdot \overrightarrow{E H}=\overrightarrow{E C} \cdot \overrightarrow{E D}$
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
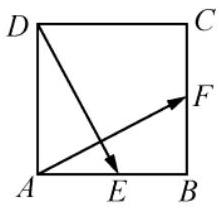
如图,在正方形 $A B C D$ 中,$E, F$ 分别是 $A B, B C$ 的中点,求证:$A F \perp D E$ .
已知 $\boldsymbol{a}=(\cos x, 2 \cos x), \boldsymbol{b}=(2 \cos x, \sin x), f(x)=\boldsymbol{a} \cdot \boldsymbol{b}$ .
(1)将函数 $f(x)$ 的图象向右平移 $\frac{\pi}{6}$ 个单位长度得到函数 $g(x)$ 的图象,求 $g(x)$ 的单调增区间;
(2)当 $\boldsymbol{a} \neq 0, \boldsymbol{a}$ 与 $\boldsymbol{b}$ 共线时,求 $f(x)$ 的值.
(3)求 $|\boldsymbol{a}-\boldsymbol{b}|$ 的最大值.
$\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b$ ,$c$ .已知向量 $\vec{m}=(\sqrt{3} b, \sqrt{3} c-2 a), \vec{n}=(\cos C, \cos B)$ ,且 $ {m} \perp {n}$ .
(1)求 $B$ ;
(2)若 $\sin A+\cos C=\sqrt{3}$ ,且 $a=3 \sqrt{3}$ ,求 $\triangle A B C$ 的周长.
(1)已知向量 $\overrightarrow{O A}=(k, 12), \overrightarrow{O B}=(4,5), \overrightarrow{O C}=(10, k)$ ,且 $A, B, C$ 三点共线,当 $k < 0$ 时,若 $k$ 为直线的斜率,则过点 $(2,-1)$ 的直线方程为
(2)若点 $O$ 和点 $F$ 分别为椭圆 $\frac{x^{2}}{4}+\frac{y^{2}}{3}=1$ 的中心和左焦点,点 $P$ 为植圆上的任意一点,则 $\overrightarrow{O P} \cdot \overrightarrow{F P}$ 的最大值为