单选题 (共 7 题 ),每题只有一个选项正确
若 $a, b, c$ 为实数,且 $a < b, c>0$ ,则下列不等关系一定成立的是
$\text{A.}$ $a+c < b+c$
$\text{B.}$ $\frac{1}{a} < \frac{1}{b}$
$\text{C.}$ $a c>b c$
$\text{D.}$ $b-a>c$
设一元二次不等式 $a x^2+b x+1>0$ 的解集为 $\{x \mid-1 < x < 2\}$ ,则 $a b$ 的值为
$\text{A.}$ -1
$\text{B.}$ $-\frac{1}{4}$
$\text{C.}$ $\frac{1}{4}$
$\text{D.}$ $-\frac{1}{2}$
已知 $a>0, b>0$ ,且 $a+2 b=1$ ,则 $\frac{1}{a}+\frac{1}{b}$ 的最小值为()
$\text{A.}$ $4 \sqrt{2}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $3-2 \sqrt{2}$
$\text{D.}$ $3+2 \sqrt{2}$
近年来受各种因素影响,国际大宗商品价格波动较大,我国某钢铁企业需要不间断从澳大利亚采购铁矿石,为保证企业利益最大化,提出以下两种采购方案。方案一:不考虑铁矿石价格升降,每次采购铁矿石的数量一定;方案二:不考虑铁矿石价格升降,每次采购铁矿石所花的钱数一定,则下列说法正确的是
$\text{A.}$ 方案一更经济
$\text{B.}$ 方案二更经济
$\text{C.}$ 两种方案一样
$\text{D.}$ 条件不足,无法确定
正实数 $x, y$ 满足 $\frac{1}{x}+\frac{4}{y}=1$ ,且不等式 $x+\frac{y}{4} \geq m^2-3 m$ 恒成立,则实数 $m$ 的取值范围(,)
$\text{A.}$ $(-4,1)$
$\text{B.}$ $(-\infty,-1) \cup(4,+\infty)$
$\text{C.}$ $[-1,4]$
$\text{D.}$ $(-\infty,-1] \cup[4,+\infty)$
"$\forall x>0, a \leq x+\frac{4}{x+2}$"的充要条件是( )
$\text{A.}$ $a>2$
$\text{B.}$ $a \geq 2$
$\text{C.}$ $a < 2$
$\text{D.}$ $a \leq 2$
若关于 $x$ 的不等式 $x^2-(m+3) x+3 m < 0$ 的解集中恰有 3 个正整数,则实数 $m$ 的取值范围为( )
$\text{A.}$ $[-2,-1)$
$\text{B.}$ $(3,4)$
$\text{C.}$ $(5,6]$
$\text{D.}$ $(6,7]$
多选题 (共 3 题 ),每题有多个选项正确
已知实数 $a, b, c$ 满足 $0 < a < b < c$ ,则下列说法正确的是( )
$\text{A.}$ $\frac{1}{a(c-a)}>\frac{1}{b(c-a)}$
$\text{B.}$ $\frac{b}{a}>\frac{b+c}{a+c}$
$\text{C.}$ $a b+c^2>a c+b c$
$\text{D.}$ $(a+b)\left(\frac{1}{a}+\frac{1}{b}\right)$ 的最小值为 4
已知关于 $x$ 的不等式 $a x^2+b x+c>0$ 的解集为 $(-\infty,-2) \cup(3,+\infty)$ ,则()
$\text{A.}$ $a>0$
$\text{B.}$ 不等式 $b x+c>0$ 的解集是 $\{x \mid x < -6\}$
$\text{C.}$ $a+b+c>0$
$\text{D.}$ 不等式 $c x^2-b x+a < 0$ 的解集为 $\left(-\infty,-\frac{1}{3}\right) \cup\left(\frac{1}{2},+\infty\right)$
已知 $\frac{1}{a}>\frac{1}{b}>0$ ,则( )
$\text{A.}$ $a^3>b^3$
$\text{B.}$ $|a|>|b|$
$\text{C.}$ $\frac{b}{a}>1$
$\text{D.}$ $\left(\frac{1}{2}\right)^a>\left(\frac{1}{2}\right)^b$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
不等式 $\frac{2 x-1}{x+2} \leq 1$ 的解集为
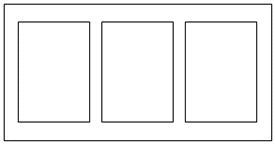
某校生物兴趣小组为开展课题研究,分得一块面积为 $32 m^2$ 的矩形空地,并计划在该空地上设置三块全等的矩形试验区(如图所示)。要求试验区四周各空 0.5 m ,各试验区之间也空 0.5 m 。则每块试验区的面积的最大值为 $\qquad$ $m ^2$ .
已知正实数 $a, b$ 满足 $a b-b+1=0$ ,则 $\frac{1}{a}+4 b$ 的最小值是
已知 $x>0, y>0$ ,且 $x+2 y=\frac{2}{x}+\frac{1}{y}+7$ ,则 $x+2 y$ 的取值范围是
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知关于 $x$ 的不等式 $a x^2-3 x+2>0$ 的解集为 $\{x \mid x < 1$ 或 $x>b\}$ .
(1)求 $a, ~ b$ 的值;
(2)当 $m>0, n>0$ 且满足 $\frac{a}{m}+\frac{b}{n}=1$ 时,有 $2 m+n \geq k^2+k+2$ 恒成立,求实数 $k$ 的范围。
设函数 $f(x)=a x^2+b x-3(a, b \in R , a \neq 0)$ ,关于 $x$ 的不等式 $f(x) < k(k$ 为常数 $)$ 的解集为 $(-3$ ,
1).
(1)若 $k=0$ ,求实数 $a, b$ 的值;
(2)当 $x \in[1,3]$ 时,$f(x) < x-2$ 恒成立,试求 $a$ 的取值范围.
关于 $x$ 的不等式 $a x^2-(a+1) x+1 < 0$
(1)若 $a=-2$ 解关于 $x$ 的不等式 $a x^2-(a+1) x+1 < 0$
(2)若 $a>0$ 解关于 $x$ 的不等式 $a x^2-(a+1) x+1 < 0$
已知函数 $f(x)=x^2+b x+c(b, c \in R)$ ,对任意的 $x \in R$ ,恒有 $f^{\prime}(x) \leq f(x)$ .
(1)证明:当 $x \geqslant 0$ 时,$f(x) \leq(x+c)^2$ ;
(2)若对满足题设条件的任意 $b, c$ ,不等式 $f(c)-f(b) \leq M\left(c^2-b^2\right)$ 恒成立,求 $M$ 的最小值.