解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设二维离散型随机变量 $(X, Y)$ 的概率分布的部分数据如下:
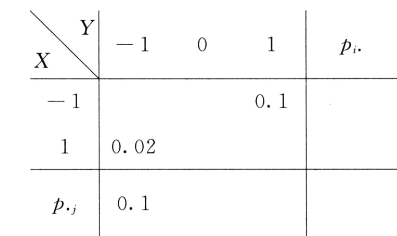
已知 $E(X)=0$, 且 $X$ 与 $Y$ 不相关.
(I) 试将分布中的其余数据填人空白处;
(II) 试问 $X$ 与 $Y$ 是否独立?
(III) 求 $\operatorname{Cov}\left(X, Y^2\right)$.
设二维正态随机变量 $(X, Y)$ 的概率密度为 $f(x, y)$. 已知条件概率密度
$$
\begin{aligned}
& f_{X \mid Y}(x \mid y)=A e^{-\frac{2}{3}\left(x-\frac{y}{2}\right)^2},-\infty < x < +\infty, \text { 和 } \\
& f_{Y \mid X}(y \mid x)=B e^{-\frac{2}{3}\left(y-\frac{x}{2}\right)^2},-\infty < y < +\infty .
\end{aligned}
$$
求 (I) 常数 $A$ 和 $B$;
(II) $X$ 和 $Y$ 的边缘概率密度 $f_X(x)$ 和 $f_Y(y)$;
(III) $f(x, y)$ 和 $\rho_{X Y}$.
已知随机变量 $X_1, X_2, X_3, X_4$ 相互独立, $X_1$ 与 $X_2$ 都在区间 $(0,1)$ 上服从均匀分布, $X_3$ 与 $X_4$ 都服从参数为 $\frac{1}{2}$ 的 $0-1$ 分布, 记 $Y=X_1+X_2+X_3 X_4$, 求 $Y$ 的分布函数 $F_Y(y)$ 及概率密度 $f_Y(y)$.
设总体 $X$ 的概率分布为
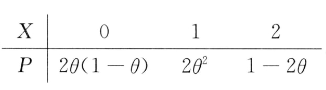
其中参数 $\theta \in\left(0, \frac{1}{2}\right)$ 未知,以 $N_i$ 表示来自总体 $X$ 的简单随机样本(样本容量为 $n$ )中等于 $i$ 的个数 $(i=0,1,2)$.
(I) 求参数 $\theta$ 的矩估计量 $\hat{\theta}$;
(II) 求常数 $a_0, a_1, a_2$, 使 $T=\sum_{i=0}^2 a_i N_i$ 为 $\theta^2$ 的无偏估计量, 并求 $T$ 的方差.
设 $X_1, X_2, \cdots, X_n$ 为来自总体 $X$ 的简单随机样本, $X$ 的概率密度为
$$
f(x)=\frac{1}{2 \lambda} e^{-\frac{|x|}{\lambda}} \quad(-\infty < x < +\infty, \lambda>0) .
$$
(I) 求参数 $\lambda$ 的矩估计量 $\hat{\lambda}_1$;
(II) 求参数 $\lambda$ 的最大似然估计量 $\hat{\lambda}_2$;
(III) 判断 $\hat{\lambda}_2$ 是否为 $\lambda$ 的无偏估计量, 并说明理由.
设随机变量 $X \sim B\left(1, \frac{1}{3}\right)$, 随机变量 $Y \sim B\left(1, \frac{1}{4}\right)$, 已知 $P\{X=0, Y=0\}=\frac{7}{12}$.求 $(I)(X, Y)$ 的概率分布;
(II) $X$ 和 $Y$ 的相关系数 $\rho$;
(III) $P\left\{X^2+Y^2=1 \mid X=1\right\}$ 和 $P\left\{X=1 \mid X^2+Y^2=1\right\}$.