设总体 $X$ 的概率分布为
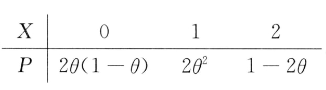
其中参数 $\theta \in\left(0, \frac{1}{2}\right)$ 未知,以 $N_i$ 表示来自总体 $X$ 的简单随机样本（样本容量为 $n$ ）中等于 $i$ 的个数 $(i=0,1,2)$.
(I) 求参数 $\theta$ 的矩估计量 $\hat{\theta}$;
(II) 求常数 $a_0, a_1, a_2$, 使 $T=\sum_{i=0}^2 a_i N_i$ 为 $\theta^2$ 的无偏估计量, 并求 $T$ 的方差.
$\text{A.}$
$\text{B.}$
$\text{C.}$
$\text{D.}$