单选题 (共 10 题 ),每题只有一个选项正确
有四个数 $3.14,3.1415926 \cdots, 0.7, \frac{4}{3}$, 其中无理数的个数为
$\text{A.}$ 3 个
$\text{B.}$ 2 个
$\text{C.}$ 1 个
$\text{D.}$ 0 个
一个数的算术平方根为 $a$, 则比这个数大 5 的数是
$\text{A.}$ $a+5$
$\text{B.}$ $a-5$
$\text{C.}$ $a^2+5$
$\text{D.}$ $a^2-5$
下列运算正确的是
$\text{A.}$ $5+\sqrt{5}=5 \sqrt{5}$
$\text{B.}$ $\sqrt{6}-\sqrt{5}=1$
$\text{C.}$ $\sqrt{8} \times \sqrt{2}=4$
$\text{D.}$ $\frac{\sqrt{8}}{\sqrt{2}}=4$
如果三角形边长分别为 $6,8,10$, 那么最短边上的高为
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ 6
$\text{D.}$ 8
下列叙述中正确的是
$\text{A.}$ 因为 $8^2=64$, 所以 64 的平方根为 8
$\text{B.}$ 因为 $-2^2=-4$, 所以 $-4$ 的算术平方根为 $-2$
$\text{C.}$ 因为 $(-3)^3=-27$, 所以 $-27$ 的立方根为 $-3$
$\text{D.}$ 0 没有立方根
若正方形的边长为 $\sqrt{2}-1$, 则此正方形的面积约是
$\text{A.}$ $0.20$
$\text{B.}$ $0.19$
$\text{C.}$ $0.18$
$\text{D.}$ $0.17$
若 $m=\sqrt{20}-3$, 则估计 $m$ 的取值范围是
$\text{A.}$ $2 < m < 3$
$\text{B.}$ $1 < m < 2$
$\text{C.}$ $3 < m < 4$
$\text{D.}$ $4 < m < 5$
在 Rt $\triangle A B C$ 中, $a: b=3: 4, c=15$ 为斜边, 则此三角形的周长为
$\text{A.}$ 30
$\text{B.}$ 36
$\text{C.}$ 48
$\text{D.}$ 50
如图, 某人欲渡一条河, 由于水流的影响, 实际上岸地点 $C$ 偏离欲到达的 $B$ 点 $240 \mathrm{~m}$, 结果他 在水中实际游了 $510 \mathrm{~m}$, 则该河的宽度为
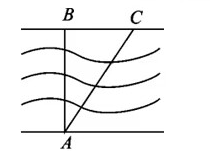
$\text{A.}$ $300 \mathrm{~m}$
$\text{B.}$ $400 \mathrm{~m}$
$\text{C.}$ $450 \mathrm{~m}$
$\text{D.}$ $480 \mathrm{~m}$
直角三角形纸片的两直角边长分别为 6,8 , 现将 $\triangle A B C$ 按如图所示方式折叠, 使点 $A$ 与点 $B$ 重合, 折痕为 $D E$, 则 $C E: C B$ 的值是
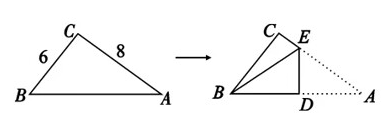
$\text{A.}$ $\frac{\sqrt{24}}{7}$
$\text{B.}$ $\frac{\sqrt{7}}{3}$
$\text{C.}$ $\frac{7}{24}$
$\text{D.}$ $\frac{1}{3}$
填空题 (共 8 题 ),请把答案直接填写在答题纸上
化简:
$\sqrt[3]{2+\frac{10}{27}}=$
$\sqrt[3]{3 \frac{3}{8}}=$
对于任意不相等的两个数 $a, b$, 定义一种新运算: $a @ b=\frac{\sqrt{a+b}}{a-b}$, 如 $3 @ 2=\frac{\sqrt{3+2}}{3-2}=\sqrt{5}$, 那么 $12 @ 4=$
已知 $|x|=5, y=3$, 则 $x-y=$
直角三角形有一条直角边为 11 , 另外两条边长是相邻的自然数, 则周长为
将 $\sqrt{\frac{5}{7}}, \frac{5}{\sqrt{7}}, \frac{\sqrt{5}}{7}$ 三个数按从小到大的顺序排列为
如图, 旗杆 $A B$ 在地面上的影长 $B C$ 为 $4 \mathrm{~m}, A B=3 \mathrm{~m}$, 则 $A C$ 为 多少 $\mathrm{m} .$
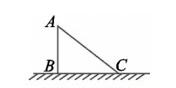
如图, 在 $\triangle A B C$ 中, $\angle A B C=90^{\circ}, C B=12, A C=13$, 则阴影部分的面积是
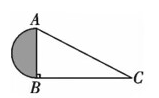
如图, Rt $\triangle A B C$ 中, $\angle B=90^{\circ}, A B=3 \mathrm{~cm}, A C=5 \mathrm{~cm}$, 将 $\triangle A B C$ 折叠, 使点 $C$ 与 $A$ 重合, 得折痕 $D E$, 则 $\triangle A B E$ 的周长等于

解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算
(1) $\sqrt{18}-\frac{2}{\sqrt{2}}-\frac{\sqrt[3]{8}}{2}+\sqrt[3]{27}$
(2) $-2^2+|4-7|+(\sqrt{3}-\pi)^0$.
已知 $a, b$ 互为相反数, $m, n$ 互为倒数, 求 $\frac{a^2-b^2}{a^2+b^2}-\sqrt{m n}$ 的值.
已知 $x, y$ 满足 $|x-4|+\sqrt{y-8}=0$, 求以 $x, y$ 的值为两边长的等腰三角形的周长.
如图, 学校 $A$ 与直线形公路 $l$ 的距离为 $3 \mathrm{~km}$, 又与该公路的某车站 $D$ 的距离为 $5 \mathrm{~km}$, 现要在公路上建一商店 $C$, 使之与该学校及车站 $D$ 的距离相等, 求商店与车站的距离.

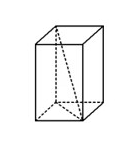
小明要把一根长 $39 \mathrm{~cm}$ 的玻璃棒装人一个长、宽、高分别是 $15 \mathrm{~cm} 、 15 \mathrm{~cm} 、 22 \mathrm{~cm}$ 的纸 盒 (如图所示). 问:能完全装进去吗? 为什么?
甲、乙两人计算 $a+\sqrt{1-2 a+a^2}$ 的值,当 $a=3$ 时,得到下面不同的答案 :
甲的解答: $a+\sqrt{1-2 a+a^2}=a+\sqrt{(1-a)^2}=a+1-a=1$.
乙的解答: $a+\sqrt{1-2 a+a^2}=a+\sqrt{(a-1)^2}=a+a-1=2 a-1=5$.
哪一个解答是正确的? 错误的解答错在哪里? 为什么?
如图, 在 $\triangle A B C$ 中, $\angle C=90^{\circ}, D$ 是 $B C$ 边上一点, $D E \perp A B$ 于点 $E, \angle A D C=45^{\circ}$, 且 $D E: A E=$ $1: 5$, 若 $D E=\sqrt{2}$, 求 $A C$ 的长.
