单选题 （共 10 题 ），每题只有一个选项正确
下列各数中，最小的是
$\text{A.}$ 2
$\text{B.}$ 1
$\text{C.}$ -1
$\text{D.}$ -2
下列无理数中, 大小在 3 与 4 之间的是
$\text{A.}$ $\sqrt{7}$
$\text{B.}$ $2 \sqrt{2}$
$\text{C.}$ $\sqrt{13}$
$\text{D.}$ $\sqrt{17}$
下列运算正确的是
$\text{A.}$ $2(a-1)=2 a-2$
$\text{B.}$ $(a+b)^2=a^2+b^2$
$\text{C.}$ $3 a+2 a=5 a^2$
$\text{D.}$ $(a b)^2=a b^2$
不等式 $x \ge 2$ 的解集在数轴上表示为
$\text{A.}$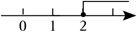 
$\text{B.}$ 
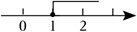$\text{C.}$ 
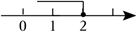$\text{D.}$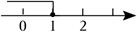 
如图是中国象棋棋盘的一部分, 建立如图所示的平面直角坐标系, 已知 "車" 所在位置的坐标为 $(-2,2)$ ，则 "炮" 所在位置的坐标为
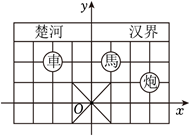
$\text{A.}$ $(3,1)$
$\text{B.}$ $(1,3)$
$\text{C.}$ $(4,1)$
$\text{D.}$ $(3,2)$
以下调查中, 适合全面调查的是
$\text{A.}$ 了解全国中学生的视力情况
$\text{B.}$ 检测 "神舟十六号" 飞船的零部件
$\text{C.}$ 检测台州的城市空气质量
$\text{D.}$ 调查某池塘中现有鱼的数量
如图, 圆$O$ 的圆心 $O$ 与正方形的中心重合, 已知圆 $O$ 的半径和正方形的边长都为 4 , 则圆上任意一点到正方形边上任意一点距离的最小值为
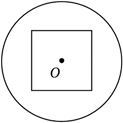
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ 2
$\text{C.}$ $4+2 \sqrt{2}$
$\text{D.}$ $4-2 \sqrt{2}$
如图, 锐角三角形 $A B C$ 中, $A B=A C$, 点 $D, E$ 分别在边 $A B, A C$ 上,连接 $B E, C D$. 下列命题中, 假命题是
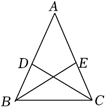
$\text{A.}$ 若 $C D=B E$, 则 $\angle D C B=\angle E B C$
$\text{B.}$ 若 $\angle D C B=\angle E B C$, 则 $C D=B E$
$\text{C.}$ 若 $B D=C E$, 则 $\angle D C B=\angle E B C$
$\text{D.}$ 若 $\angle D C B=\angle E B C$, 则 $B D=C E$
抛物线 $y=a x^2-a(a \neq 0)$ 与直线 $y=k x$ 交于 $A\left(x_1, y_1\right), B\left(x_2, y_2\right)$ 两点,若 $x_1+x_2 < 0$, 则直线 $y=a x+k$ 一定经过
$\text{A.}$ 第一、二象限
$\text{B.}$ 第二、三象限
$\text{C.}$ 第三、四象限
$\text{D.}$ 第一、四象限
填空题 （共 6 题 ），请把答案直接填写在答题纸上
一个不透明的口袋中有 5 个除颜色外完全相同的小球, 其中 2 个红球, 3 个白球. 随机摸出一个小球, 摸出红球的概率是
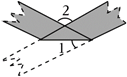
用一张等宽的纸条折成如图所示的图案, 若 $\angle 1=20^{\circ}$, 则 $\angle 2$ 的度数为 .
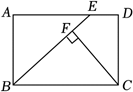
如图, 矩形 $A B C D$ 中, $A B=4, A D=6$. 在边 $A D$ 上取一点 $E$, 使 $B E=B C$,过点 $C$ 作 $C F \perp B E$, 垂足为点 $F$, 则 $B F$ 的长为
3 月 12 日植树节期间, 某校环保小卫士组织植树活动. 第一组植树 12 棵; 第二组比第一组多 6 人, 植树 36 棵; 结果两组平均每人植树的棵数相等,则第一组有 $\qquad$人。
如图, 点 $C, D$ 在线段 $A B$ 上 (点 $C$ 在点 $A, D$ 之间), 分别以 $A D$, $B C$ 为边向同侧作等边三角形 $A D E$ 与等边三角形 $C B F$, 边长分别为 $a, b, C F$ 与 $D E$ 交于点 $H$, 延长 $A E, B F$ 交于点 $G, A G$ 长为 $c$.
(1) 若四边形 $E H F G$ 的周长与 $\triangle C D H$ 的周长相等, 则 $a, b, c$ 之间的等量关系为 $\qquad$ ；
(2) 若四边形 $E H F G$ 的面积与 $\triangle C D H$ 的面积相等, 则 $a, b, c$ 之间的等量关系为 . $\qquad$
解答题 （共 8 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $2^2+|-3|-\sqrt{25}$.
解方程组: $\left\{\begin{array}{l}x+y=7 \\ 2 x-y=2\end{array}\right.$.
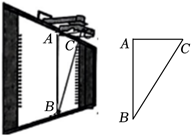
教室里的投影仪投影时, 可以把投影光线 $C A, C B$ 及在黑板上的投影图象高度 $A B$ 抽象成如图所示的 $\triangle A B C, \angle B A C=90^{\circ}$, 黑板上投影图象的高度 $A B=120 \mathrm{~cm}, C B$ 与 $A B$ 的夹角 $\angle B=33.7^{\circ}$, 求 $A C$ 的长. (结果精确到 1 cm . 参考数据: $\sin 33.7^{\circ} \approx 0.55, \cos 33.7^{\circ} \approx 0.83, \tan 33.7^{\circ} \approx 0.67$ )
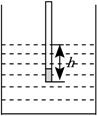
科学课上, 同学用自制密度计测量液体的密度. 密度计悬浮在不同的液体中时, 浸在液体中的高度 $h$ (单位: cm ) 是液体的密度 $\rho$ (单位: $\mathrm{g} / \mathrm{cm}^3$ )的反比例函数, 当密度计悬浮在密度为 $1 \mathrm{~g} / \mathrm{cm}^3$ 的水中时, $h=20 \mathrm{~cm}$.
(1) 求 $h$ 关于 $\rho$ 的函数解析式;
(2) 当密度计悬浮在另一种液体中时, $h=25 \mathrm{~cm}$, 求该液体的密度 $\rho$.
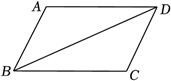
如图, 四边形 $A B C D$ 中, $A D / / B C, \angle A=\angle C, B D$ 为对角线.
(1) 证明: 四边形 $A B C D$ 是平行四边形;
(2) 已知 $A D>A B$, 请用无刻度的直尺和圆规作菱形 $B E D F$, 顶点 $E, F$ 分别在边 $B C, A D$ 上 (保留作图痕迹, 不要求写作法).
为了改进几何教学，张老师选择 A，B 两班进行教学实验研究，在实验班B 实施新的教学方法，在控制班A 采用原来的教学方法．在实验开始前，进行一次几何能力测试（前测，总分25分），经过一段时间的教学后，再用难度、题型、总分相同的试卷进行测试（后测），得到前测和后测数据并整理成表1和表2．
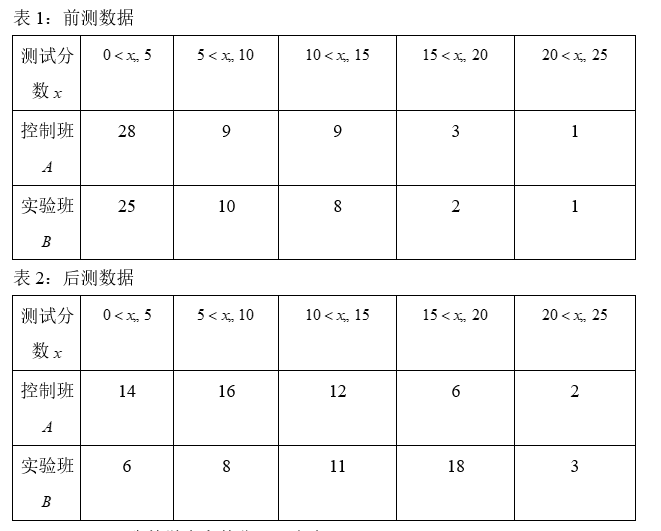
(1) $A, B$ 两班的学生人数分别是多少?
(2) 请选择一种适当的统计量, 分析比较 $A, B$ 两班的后测数据.
(3) 通过分析前测、后测数据, 请对张老师的教学实验效果进行评价.
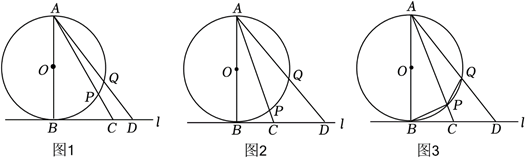
我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系，用直线上点的位置刻画圆上点的位置．如图，$AB$ 是$\ \odot O$ 的直径，直线$l$是$\ \odot O$ 的切线，$B$ 为切点．$P$ ，$Q$ 是圆上两点（不与点 重合，且在直径 的同侧）， 分别作射线 $A P$, $A Q$ 交直线 $l$ 于点 $C$, 点 $D$.
(1) 如图 1, 当 $A B=6, B P$ 长为 $\pi$ 时, 求 $B C$ 的长;
(2) 如图 2, 当 $\frac{A Q}{A B}=\frac{3}{4}, B P=P Q$ 时, 求 $\frac{B C}{C D}$ 的值;
(3) 如图 3, 当 $\sin \angle B A Q=\frac{\sqrt{6}}{4}, B C=C D$ 时, 连接 $B P, P Q$, 直接写出 $\frac{P Q}{B P}$ 的值.
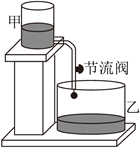
【问题背景】“刻漏”是我国古代的一种利用水流计时的工具．综合实践小组准备用甲、乙两个透明的竖直放置的容器和一根带节流阀（控制水的流速大小）的软管制作简易计时装置．
【实验操作】综合实践小组设计了如下的实验：先在甲容器里加满水，此时水面高度为 ，开始放水后每隔 观察一次甲容器中的水面高度，获得的数据如表：
任务 1：分别计算表中每隔 $10 \min$ 水面高度观察值的变化量.
【建立模型】小组讨论发现: " $t=0, h=30$ " 是初始状态下的准确数据, 水面高度值的变化不均匀, 但可以用一次函数近似地刻画水面高度 $h$ 与流水时间 $t$ 的关系。
任务 2: 利用 $t=0$ 时, $h=30 ; t=10$ 时, $h=29$ 这两组数据求水面高度 $h$ 与流水时间 $t$ 的函数解析式;
【反思优化】经检验, 发现有两组表中观察值不满足任务 2 中求出的函数解析式, 存在偏差, 小组决定优化函数解析式, 减少偏差. 通过查阅资料后知道: $t$为表中数据时, 根据解析式求出所对应的函数值, 计算这些函数值与对应 $h$ 的观察值之差的平方和, 记为 $w ; w$ 越小, 偏差越小.
任务 3：（1）计算任务 2 得到的函数解析式的 $w$ 值;
(2) 请确定经过 $(0,30)$ 的一次函数解析式, 使得 $w$ 的值最小;
【设计刻度】得到优化的函数解析式后, 综合实践小组决定在甲容器外壁设计刻度，通过刻度直接读取时间.
任务 4: 请你简要写出时间刻度的设计方案.
