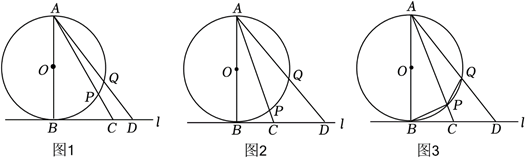
我们可以通过中心投影的方法建立圆上的点与直线上点的对应关系,用直线上点的位置刻画圆上点的位置.如图,$AB$ 是$\ \odot O$ 的直径,直线$l$是$\ \odot O$ 的切线,$B$ 为切点.$P$ ,$Q$ 是圆上两点(不与点 重合,且在直径 的同侧), 分别作射线 $A P$, $A Q$ 交直线 $l$ 于点 $C$, 点 $D$.
(1) 如图 1, 当 $A B=6, B P$ 长为 $\pi$ 时, 求 $B C$ 的长;
(2) 如图 2, 当 $\frac{A Q}{A B}=\frac{3}{4}, B P=P Q$ 时, 求 $\frac{B C}{C D}$ 的值;
(3) 如图 3, 当 $\sin \angle B A Q=\frac{\sqrt{6}}{4}, B C=C D$ 时, 连接 $B P, P Q$, 直接写出 $\frac{P Q}{B P}$ 的值.
(1) 如图 1, 当 $A B=6, B P$ 长为 $\pi$ 时, 求 $B C$ 的长;
(2) 如图 2, 当 $\frac{A Q}{A B}=\frac{3}{4}, B P=P Q$ 时, 求 $\frac{B C}{C D}$ 的值;
(3) 如图 3, 当 $\sin \angle B A Q=\frac{\sqrt{6}}{4}, B C=C D$ 时, 连接 $B P, P Q$, 直接写出 $\frac{P Q}{B P}$ 的值.
