单选题 (共 14 题 ),每题只有一个选项正确
设全集 $I=\{0,1,2,3,4\}$, 集合 $A=\{0,1,2,3\}$, 集合 $B=\{2,3,4\}$, 则 $\bar{A} \cup \bar{B}$
$\text{A.}$ $\{0\}$
$\text{B.}$ $\{0,1\}$
$\text{C.}$ $\{0,1,4\}$
$\text{D.}$ $\{0,1,2,3,4\}$
如果方程 $x^2+k y^2=2$ 表示焦点在 $y$ 轴上的椭圆,那么实数 $k$ 的取值范围是
$\text{A.}$ $(0,+\infty)$
$\text{B.}$ $(0,2)$
$\text{C.}$ $(1,+\infty)$
$\text{D.}$ $(0,1)$
极坐标方程 $\rho=\cos \left(\frac{\pi}{4}-\theta\right)$ 所表示的曲线是
$\text{A.}$ 双曲线
$\text{B.}$ 椭圆
$\text{C.}$ 抛物线
$\text{D.}$ 圆
设 $\theta$ 是第二象限的角, 则必有
$\text{A.}$ $\operatorname{tg} \frac{\theta}{2}>\operatorname{ctg} \frac{\theta}{2}$
$\text{B.}$ $\operatorname{tg} \frac{\theta}{2} < \operatorname{ctg} \frac{\theta}{2}$
$\text{C.}$ $\sin \frac{\theta}{2}>\cos \frac{\theta}{2}$
$\text{D.}$ $\sin \frac{\theta}{2} < \cos \frac{\theta}{2}$
某种细菌在培养过程中, 每 20 分钟分裂一次 (一个分裂为两个). 经过 3 小时, 这种细菌由 1 个可繁殖成
$\text{A.}$ 511 个
$\text{B.}$ 512 个
$\text{C.}$ 1023 个
$\text{D.}$ 1024 个
在下列函数中, 以 $\frac{\pi}{2}$ 为周期的函数是
$\text{A.}$ $y=\sin 2 x+\cos 4 x$
$\text{B.}$ $y=\sin 2 x \cos 4 x$
$\text{C.}$ $y=\sin 2 x+\cos 2 x$
$\text{D.}$ $y=\sin 2 x \cos 2 x$
已知正六棱台的上、下底面边长分别为 2 和 4 , 高为 2 , 则其体积为
$\text{A.}$ $32 \sqrt{3}$
$\text{B.}$ $28 \sqrt{3}$
$\text{C.}$ $24 \sqrt{3}$
$\text{D.}$ $20 \sqrt{3}$
设 $F_1$ 和 $F_2$ 为双曲线 $\frac{x^2}{4}-y^2=1$ 的两个焦点, 点 $P$ 在双曲线上且满足 $\angle F_1 P F_2=90^{\circ}$,则 $\triangle F_1 P F_2$ 的面积是
$\text{A.}$ 1
$\text{B.}$ $\frac{\sqrt{5}}{2}$
$\text{C.}$ 2
$\text{D.}$ $\sqrt{5}$
如果复数 $z$ 满足 $|z+i|+|z-i|=2$, 那么 $|z+i+1|$ 的最小值是
$\text{A.}$ 1
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ 2
$\text{D.}$ $\sqrt{5}$
有甲、乙、丙三项任务, 甲需 2 人承担, 乙、丙各需 1 人承担. 从 10 人中选派 4 人承担这三项任务, 不同的选法共有
$\text{A.}$ 1260 种
$\text{B.}$ 2025 种
$\text{C.}$ 2520 种
$\text{D.}$ 5040 种
对于直线 $m 、 n$ 和平面 $a 、 \beta, a \perp \beta$ 的一个充分条件是
$\text{A.}$ $m \perp n, m / / a, n / / \beta$
$\text{B.}$ $m \perp n, \quad a \cap \beta=m, \quad n \subset a$
$\text{C.}$ $m / / n, n \perp \beta$, $m \subset a$
$\text{D.}$ $m / / n, m \perp a, n \perp \beta$
已知过球面上 $A 、 B 、 C$ 三点的截面和球心的距离等于球半径的一半, 且 $A B=B C=C A=2$, 则球面面积是
$\text{A.}$ $\frac{16}{9} \pi$
$\text{B.}$ $\frac{8}{3} \pi$
$\text{C.}$ $4 \pi$
$\text{D.}$ $\frac{64}{9} \pi$
函数 $y=\arccos (\sin x)\left(-\frac{\pi}{3} < x < \frac{2 \pi}{3}\right)$ 的值域是
$\text{A.}$ $\left(\frac{\pi}{6}, \frac{5 \pi}{6}\right)$
$\text{B.}$ $\left[0, \frac{5 \pi}{6}\right)$
$\text{C.}$ $\left(\frac{\pi}{3}, \frac{2 \pi}{3}\right)$
$\text{D.}$ $\left[\frac{\pi}{6}, \frac{2 \pi}{3}\right)$
定义在 $(-\infty,+\infty)$ 上的任意函数 $f(x)$ 都可以表示成一个奇函数 $g(x)$ 和一个偶函数 $h(x)$ 之和, 如果 $f(x)=\lg \left(10^x+1\right), x \in(-\infty,+\infty)$, 那么
$\text{A.}$ $g(x)=x, \quad h(x)=\lg \left(10^x+10^{-x}+2\right)$
$\text{B.}$ $g(x)=\frac{1}{2}\left[\lg \left(10^x+1\right)+x\right], \quad h(x)=\frac{1}{2}\left[\lg \left(10^x+1\right)-x\right]$
$\text{C.}$ $g(x)=\frac{x}{2}, h(x)=\lg \left(10^x+1\right)-\frac{x}{2}$
$\text{D.}$ $g(x)=-\frac{x}{2}, h(x)=\lg \left(10^x+1\right)+\frac{x}{2}$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
在 $(3-x)^7$ 的展开式中, $x^5$ 的系数是 $\qquad$ . (用数字作答)
抛物线 $y^2=8-4 x$ 的准线方程是 $\qquad$ , 圆心在该抛物线的顶点且与其准线相切的圆的方程是
设圆锥底面圆周上两点 $A 、 B$ 间的距离为 2 , 圆锥顶点到直线 $A B$ 的距离为 $\sqrt{3}$, $A B$ 和圆锥的轴的距离为 1 , 则该圆锥的体积为
在测量某物理量的过程中, 因仪器和观察的误差, 使得 $n$ 次测量分别得到 $a_1$, $a_2, \cdots a_n$, 共 $n$ 个数据, 我们规定所测量物理量的 “最佳近似值” $a$ 是这样一个量: 与其他近似值比较, $a$ 与各数据的差的平方和最小. 依此规定, 从 $a_1, a_2, \cdots, a_n$ 推出的 $a=$
已知 $\sin \theta+\cos \theta=\frac{1}{5}, \theta \in(0, \pi)$, 则 $\operatorname{ctg} \theta$ 的值是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $z=1+i$.
(1) 设 $\omega=z^2+3 \bar{z}-4$, 求 $\omega$ 的三角形式;
(2) 如果 $\frac{z^2+a z+b}{z^2-z+1}=1-i$, 求实数 $a, b$ 的值.
已知函数 $f(x)=\operatorname{tg} x, x \in\left(0, \frac{\pi}{2}\right)$. 若 $x_1, x_2 \in\left(0, \frac{\pi}{2}\right)$, 且 $x_1 \neq x_2$, 证明 $\frac{1}{2}\left[f\left(x_1\right)+f\left(x_2\right)\right]>f\left(\frac{x_1+x_2}{2}\right)$
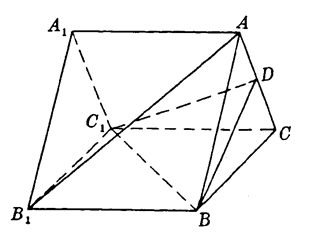
如图, 已知 $A_1 B_1 C_1-A B C$ 是正三棱柱, $D$ 是 $A C$ 中点.
(1) 证明 $A B_1 / /$ 平面 $D B C_1$;
(2) 假设 $A B_1 \perp B C_1$, 求以 $B C_1$ 为棱, $D B C_1$ 与 $C B C_1$ 为面的二面角 $a$ 的度数.
已知直线 1 过坐标原点, 抛物线 $C$ 顶点在原点, 焦点在 $X$ 轴正半轴上. 若点 $A(-1,0)$ 和点 $B(0,8)$ 关于 $l$ 的对称点都在 $C$ 上,求直线 $l$ 和拋物线 $C$ 的方程.
设 $\left\{a_n\right\}$ 是正数组成的数列, 其前 $n$ 项和为 $S_n$, 并且对于所有的自然数 $n, a_n$ 与 2 的等差中项等于 $S_n$ 与 2 的等比中项.
(1) 写出数列 $\left\{a_n\right\}$ 的前 3 项;
(2) 求数列 $\left\{a_n\right\}$ 的通项公式 (写出推证过程);
(3) 令 $b_n=\frac{1}{2}\left(\frac{a_{n+1}}{a_n}+\frac{a_n}{a_{n+1}}\right)(n \in \mathbf{N})$, 求 $\lim _{n \rightarrow \infty}\left(b_1+b_2+... +b_n-n\right)$.
求函数 $y=\frac{\sin 3 x \sin ^3 x+\cos 3 x \cos ^3 x}{\cos ^2 2 x}+\sin 2 x$ 的最小值.