单选题 （共 10 题 ），每题只有一个选项正确
下列互为倒数的是（）
$\text{A.}$ 3 和 $\frac{1}{3}$
$\text{B.}$ $-2$ 和 2
$\text{C.}$ 3 和 $-\frac{1}{3}$
$\text{D.}$ $-2$ 和 $\frac{1}{2}$
主视图和左视图一样的是
$\text{A.}$ 
$\text{B.}$ 
$\text{C.}$ 
$\text{D.}$ 
某学校进行演讲比赛, 最终有 7 位同学进入决赛, 这七位同学的评分分别是 $9.5,9.3,9.1,9.4,9.7$, 9.3, 9.6. 请问这组评分的众数是
$\text{A.}$ $9.5$
$\text{B.}$ $9.4$
$\text{C.}$ $9.1$
$\text{D.}$ $9.3$
某公司一年的销售利润是 $1.5$ 万亿元。 $1.5$ 万亿用科学记数法表示为
$\text{A.}$ $0.15 \times 10^{13}$
$\text{B.}$ $1.5 \times 10^{12}$
$\text{C.}$ $1.5 \times 10^{13}$
$\text{D.}$ $15 \times 10^{12}$
下列运算正确的是
$\text{A.}$ $a^{2} \cdot a^{6}=a^{8}$
$\text{B.}$ $(-2 a)^{3}=6 a^{3}$
$\text{C.}$ $2(a+b)=2 a+b$
$\text{D.}$ $2 a+3 b=5 a b$
一元一次不等式组 $ \left\{\begin{array}{l}
x-1 \geq 0 \\
x < 2
\end{array}\right. $ 的解集为
$\text{A.}$ 
$\text{B.}$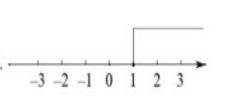 
$\text{C.}$ 
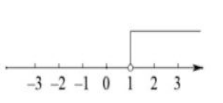$\text{D.}$ 
一副三角板如图所示放置, 斜边平行, 则 $\angle 1$ 的度数为
$\text{A.}$ $5^{\circ}$
$\text{B.}$ $10^{\circ}$
$\text{C.}$ $15^{\circ}$
$\text{D.}$ $20^{\circ}$
下列说法错误的是
$\text{A.}$ 对角线垂直且互相平分的四边形是菱形
$\text{B.}$ 同圆或等圆中, 同弧对应的圆周角相等
$\text{C.}$ 对角线相等的四边形是矩形
$\text{D.}$ 对角线垂直且相等的四边形是正方形
张三经营了一家草场, 草场里面种植有上等草和下等草。他卖五捆上等草的根数减去 11 根, 就等于 七捆下等草的根数; 卖七捆上等草的根数减去 25 根, 就等于五捆下等草的根数。设上等草一捆为 $\mathrm{x}$ 根, 下等 草一捆为 $\mathrm{y}$ 根, 则下列方程正确的是
$\text{A.}$ $\left\{\begin{array}{l}5 y-11=7 x \\ 7 y-25=5 x\end{array} \quad\right.$
$\text{B.}$ $\left\{\begin{array}{l}5 x+11=7 y \\ 7 x+25=5 y\end{array} \quad\right.$
$\text{C.}$ $\left\{\begin{array}{l}5 x-11=7 y \\ 7 x-25=5 y\end{array} \quad\right.$
$\text{D.}$ $\left\{\begin{array}{l}7 x-11=5 y \\ 5 x-25=7 y\end{array}\right.$
已知三角形 $\mathrm{ABE}$ 为直角三角形, $\angle \mathrm{ABE}=90^{\circ}, \mathrm{BC}$ 为圆 $\mathrm{O}$ 切线, $\mathrm{C}$ 为切点, $\mathrm{CA}=\mathrm{CD}$, 则 $\triangle \mathrm{ABC}$ 和 $\triangle$ $\mathrm{CDE}$ 面积之比为（）
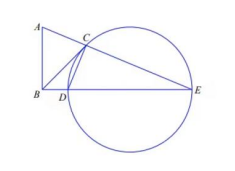
$\text{A.}$ $1: 3$
$\text{B.}$ $1: 2$
$\text{C.}$ $\sqrt{2}: 2$
$\text{D.}$ $1: 5$
填空题 （共 5 题 ），请把答案直接填写在答题纸上
某工厂一共有 1200 人, 为选拔人才, 提出了一些选拔的条件, 并进行了抽样调查。从中抽出 400 人, 发现有 300 人是符合条件的, 那么则该工厂 1200 人中符合选拔条件的人数为
已知一元二次方程 $x^{2}+6 x+m=0$ 有两个相等的实数根, 则 $m$ 的值为
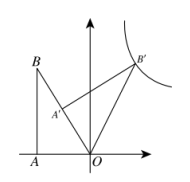
如图, 已知直角三角形 $\mathrm{ABO}$ 中 $\mathrm{AO}=1$, 将 $\triangle \mathrm{ABO}$ 绕 $\mathrm{O}$ 点旋转至 $\triangle \mathrm{ABO}$ 的位置, 且 $\mathrm{A}$ 在 $\mathrm{OB}$ 中点 $\mathrm{B}$ 在反比例函数 $\mathrm{y}=\frac{\mathrm{k}}{x}$ 上, 则 $\mathrm{k}$ 的值
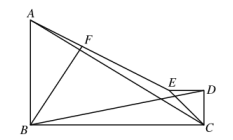
已知 $\triangle \mathrm{ABC}$ 是直角三角形, $\angle \mathrm{B}=90^{\circ}, \mathrm{AB}=3, \mathrm{BC}=5, \mathrm{AE}=2 \sqrt{5}$, 连接 $\mathrm{CE}$ 以 $\mathrm{CE}$ 为底作直角三角形 $\mathrm{CDE}$ 且 $\mathrm{CD}=\mathrm{DE}$ 。 $\mathrm{F}$ 是 $\mathrm{AE}$ 边上的一点, 连接 $\mathrm{BD}$ 和 $\mathrm{BF}, \mathrm{BD}$ 且 $\angle \mathrm{FBD}=45^{\circ}$, 则 $\mathrm{AF}$ 长为
解答题 （共 7 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $(\pi-1)^{0}-\sqrt{9}+2 \cos 45^{\circ}+\left(\frac{1}{5}\right)^{-1}$.
化简求值: $\left(\frac{2 x-2}{x}-1\right) \div \frac{x^{2}-4 x+4}{x^{2}-x}$, 其中$x=4$
某工厂进行厂长选拔, 从中抽出一部分人进行箜选, 其中有 “优秀”, “良好”, “合格”,
“不合格”.
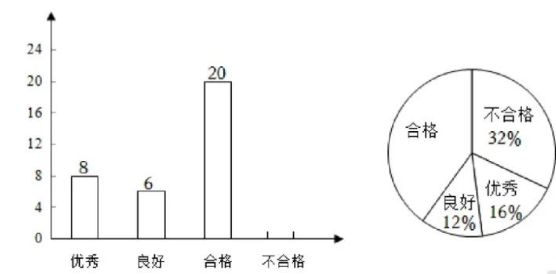
(1) 本次抽查总人数为, “合格”人数的百分比为
(2) 补全条形统计图
(3) 扇形统计图中 “不合格人数” 的度数为
在 “优秀” 中有甲乙丙三人，现从中抽出两人, 则刚好抽中甲乙两人的概率为
某学校打算购买甲乙两种不同类型的笔记本. 已知甲种类型的电脑的单价比乙种类型的要便宜 10 元, 且用 110 元购买的甲种类型的数量与用 120 元购买的乙种类型的数量一样.
(1) 求甲乙两种类型笔记本的单价.
（2）该学校打算购买甲乙两种类型笔记本共 100 件, 且购买的乙的数量不超过甲的 3 倍, 则购买的最低费 用是多少?
二次函数 $ y=\frac{1}{2} x^{2} $ 先向上平移 6 个单位, 再向右平移 3个单位, 点坐标的变化如表格所示，用光滑的曲线画在平面直角坐标系上.
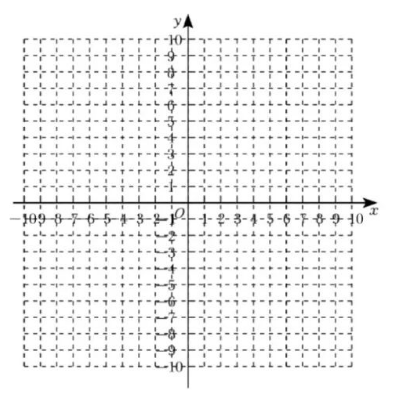
（1） $m$ 的值为
（2）在坐标系中画出平移后的图象并求出 $y=-\frac{1}{2} x^{2}+5$ 与 $y=\frac{1}{2} x^{2}$ 的交点坐标;
（3）点 $P\left(x_{1}, y_{1}\right), Q\left(x_{2}, y_{2}\right)$ 在新的函数图象上, 且 $P, Q$ 两点均在对称轴的同一侧, 若 $y_{1}>y_{2}$, 则 $x_{1}$ （ ） $x_{2}$
(填写 > 或 < 或 = ）
一个玻璃球体近似半圆 $O, A B$ 为直径, 半圆 $O$ 上点 $C$ 处有个吊灯 $E F, E F / / A B, C O \perp A B, E F$ 的中 点为 $D, O A=4$.
(1) 如图①, $\mathrm{CM}$ 为一条拉线, $\mathrm{M}$ 在 $\mathrm{OB}$ 上, $\mathrm{OM}=1.6, \mathrm{DF}=0.8$, 求 $\mathrm{CD}$ 的长度.
(2) 如图②一个玻璃镜与圆 $\mathrm{O}$ 相切, $\mathrm{H}$ 为切点, $\mathrm{M}$ 为 $\mathrm{OB}$ 上一点, $\mathrm{MH}$ 为 入射光线, $\mathrm{NH}$ 为反射光线, $\angle \mathrm{OHM}=\angle \mathrm{OHN}=45^{\circ}, \tan \angle \mathrm{COH}=\frac{3}{4}$, 求 $\mathrm{ON}$ 的长度.
(3) 如图③, M 是线段 $\mathrm{OB}$ 上的动点, $\mathrm{MH}$ 为入射光线, $\angle \mathrm{HOM}=50^{\circ}, \mathrm{HN}$ 为反射光线交圆 $\mathrm{O}$ 于点 $\mathrm{N}$, 在 $\mathrm{M}$ 从 $\mathrm{O}$ 运动到 $\mathrm{B}$ 的过程中, 求 $\mathrm{N}$ 点的运动路径长
(1) 发现: 如图①所示, 在正方形 $\mathrm{ABCD}$ 中, $\mathrm{E}$ 为 $\mathrm{AD}$ 边上一点, 将 $\triangle \mathrm{AEB}$ 沿 $\mathrm{BE}$ 翻折到 $\triangle \mathrm{BEF}$ 处, 延长 $\mathrm{EF}$ 交 $\mathrm{CD}$ 边于 $\mathrm{G}$ 点。求证： $\triangle \mathrm{BFG} \cong \triangle \mathrm{BCG}$.
(2) 探究: 如图②, 在矩形 $\mathrm{ABCD}$ 中, $\mathrm{E}$ 为 $\mathrm{AD}$ 边上一点, 且 $\mathrm{AD}=8, \mathrm{AB}=6$ 。将 $\triangle \mathrm{AEB}$ 沿 $\mathrm{BE}$ 翻折到 $\triangle \mathrm{BEF}$ 处, 延长 $\mathrm{EF}$ 交 $\mathrm{BC}$ 边于 $\mathrm{G}$ 点, 延长 $\mathrm{BF}$ 交 $\mathrm{CD}$ 边于点 $\mathrm{H}$, 且 $\mathrm{FH}=\mathrm{CH}$, 求 $\mathrm{AE}$ 的长.
(3) 拓展: 如图③, 在菱形 $\mathrm{ABCD}$ 中, $\mathrm{E}$ 为 $\mathrm{CD}$ 边上的三等分点, $\angle \mathrm{D}=60 \%$ 将 $\triangle \mathrm{ADE}$ 沿 $\mathrm{AE}$ 翻折得到 $\triangle \mathrm{AFE}$, 直线 $E F$ 交 $B C$ 于点 $P$, 求 $P C$ 的长.
