二次函数 $ y=\frac{1}{2} x^{2} $ 先向上平移 6 个单位, 再向右平移 3个单位, 点坐标的变化如表格所示，用光滑的曲线画在平面直角坐标系上.





（1） $m$ 的值为
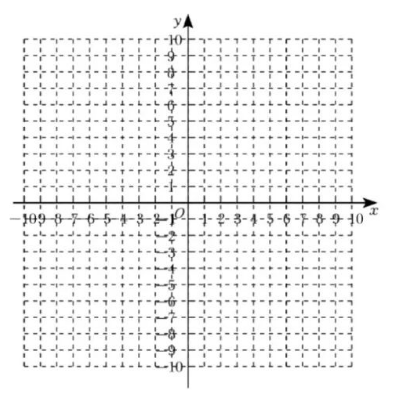
（2）在坐标系中画出平移后的图象并求出 $y=-\frac{1}{2} x^{2}+5$ 与 $y=\frac{1}{2} x^{2}$ 的交点坐标;

（3）点 $P\left(x_{1}, y_{1}\right), Q\left(x_{2}, y_{2}\right)$ 在新的函数图象上, 且 $P, Q$ 两点均在对称轴的同一侧, 若 $y_{1}>y_{2}$, 则 $x_{1}$ （　　） $x_{2}$
(填写 > 或 < 或 = ）