在坐标系 $x O y$ 中，正方形 $A B C D$ 的顶点 $A ， B$ 在 $x$ 轴上， $C(2,-3) ， D(-1,-3)$. 抛物线 $y=a x^2-2 a x+c(a>0)$ 与 $x$ 轴交于点 $E(-2,0)$ 和点 $F$.

(1)如图1，若抛物线过点 $C$ ，求抛物线的表达式和点 $F$ 的坐标.
(2)如图2，在 (1) 的条件下，连接 $C F$ ，作直线 $C E$ ，平移线段 $C F$ ，使点 $C$ 的对应点 $P$ 落在直线 $C E$ 上，点 $F$ 的对应点 $Q$ 落在抛物线上，求点 $Q$ 的坐标.
(3) 若抛物线 $y=a x^2-2 a x+c(a>0)$ 与正方形 $A B C D$ 恰有两个交点，直接写出 $a$ 的取值范围.

平面直角坐标系中，抛物线 $\mathrm{y}=-\frac{1}{3} x^2+a x+b(a$ ，均为常数）与 $\mathrm{y}$ 轴相交于点 $\mathrm{A}$ ，与 $x$ 轴相交于 $\mathrm{B}(-3 \sqrt{3}, 0), C(\sqrt{3}, 0)$ 两点，连接 $A B ，$ 过点 $C$ 作 $C D // A B$ 交抛物线于点 $D$.

(1) 求出该抛物线的函数表达式及点 $\mathrm{D}$ 的坐标;
(2) 如图1，已知点 $G$ 是线段 $A B$ 上方抛物线上一点，过点 $G$ 作 $G P \| y$ 轴交 $C D 于 P$ ，在线段 $A C$ 和线段 $C D$ 上分别有两个动点 $K 、 L$ ，且满足 $K L=2 ， M$ 是 $K L$ 的中点，当 $G P+D P$ 取得最大值时，在线段 $A B$ 上是否存在一点 $R$ ，使得 $R P+R M$ 的值最小? 若存在，请求出 $P$点的坐标以及 $R P+R M$ 的最小值; 若不存在，请说明理由.
(3) 如图2， $E$ 是线段 $B O$ 上一定点，且满足 $O E: O B=4 \sqrt{3}: 9$ ，连接 $A E$ ，将线段AE沿 $y$ 轴向下平移 6 个单位至 $H F$ ，连接 $E F ， T$是线段EF上一动点，点A、H同时绕点T逆时针旋转 $90^{\circ}$ ，应对点分别是 $A^{\prime} 、 H^{\prime}$ 。在旋转过程中，当 $\Delta E A^{\prime} H^{\prime}$ 是直角三角形时，请直接写出此时A'的坐标.

如图，直线 $y=\frac{3}{4} x+3$ 与 $x$ 轴、 $\mathrm{y}$ 轴分别交于 $\mathrm{A} 、 \mathrm{~B}$ 两点，抛物线 $y=\frac{3}{4} x^2+b x+c$ 经过 $\mathrm{A} 、 \mathrm{~B}$ 两点.

（1）求抛物线的表达式；
（2）点 $\mathrm{D}$ 是抛物线在第二象限内的点，过点 $\mathrm{D}$ 作 $x$ 轴的平行线与直线 $\mathrm{AB}$ 交于点 $\mathrm{C}$ ，求 $\mathrm{DC}$ 的长的最大值;
(3) 点 $Q$ 是线段 $A O$ 上的动点，点 $P$ 是抛物线在第一象限内的动点，连结 $P Q$ 交 $y$ 轴于点 $N$. 是否存在点 $P$ ，使 $\triangle A B Q$ 与 $\triangle B Q N$ 相似，若存在，求出点P的坐标; 若不存在，说明理由.

如图, 抛物线 $y=-\frac{1}{2} x^2+b x+c$ 与 $x$ 轴交于 $A, B(1,0)$ 两点, 与 $y$ 轴交于点 $C(0,2)$,连接 $A C$.
（1）求该抛物线的函数表达式及点 $A$ 的坐标;
( 2 ) 求 $D$ 抛是 $x$ 线轴上方抛物线上的动点, 过点 $D$ 作 $D E \perp x$ 轴于点 $E$, 是否存在点 $D$, 使得以 $B 、 D 、 E$ 为顶点的三角形与 $\triangle A O C$ 相似 (含全等)？若存在, 求出点 $D$ 的坐标；若不存在, 请说明理由.

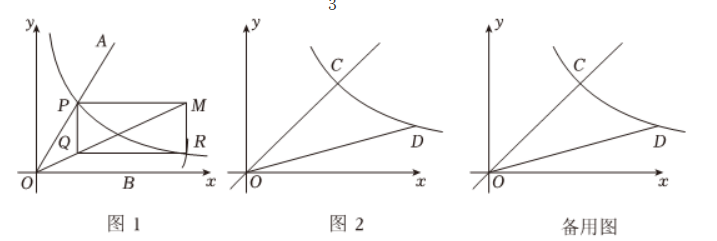
阅读材料: “三等分角” 是数学史上一个著名问题. 今天人们已经知道, 仅用圆规和直尺是不可能作出的. 在研究这个问题的过程中, 数学家帕普斯借助函数给出了一种“三等分锐角”的方法, 如图1, 步骤如下:
(1)建立直角坐标系, 将已知锐角 $\angle A O B$ 的顶点与原点 $O$ 重合, 角的一边 $O B$ 与 $x$ 轴正方向重合；
(2)在直角坐标系中, 绘制函数 $y=\frac{1}{x}$ 的图象, 图象与已知角的另一边 $O A$ 交于点 $P$;
(3)以 $P$ 为圆心、以 $2 O P$ 为半径作弧, 交函数 $y=\frac{1}{x}$ 的图象于点 $R$;
(4)分别过点 $P$ 和 $R$ 作 $x$ 轴和 $y$ 轴的平行线, 分别交于点 $M$, 点 $Q$;
(5)连接 $O M$, 得到 $\angle M O B$. 则 $\angle M O B=\frac{1}{3} \angle A O B$.

思考问题:
（1）设 $P\left(a, \frac{1}{a}\right), R\left(b, \frac{1}{b}\right)$, 求直线 $O M$ 的函数解析式 (用含 $a, b$ 的代数式表示)，并说明 $Q$ 点在直线 $O M$ 上；
(2) 证明: $\angle M O B=\frac{1}{3} \angle A O B$.
(3) 如图 2 , 若直线 $y=x$ 与反比例函数 $y=\frac{4}{x}(x \neq 0)$ 交于点 $C, D$ 为反比例函数 $y=\frac{4}{x}(x \neq 0)$ 第一象限上的一个动点, 使得 $\angle C O D=3$ $0^{\circ}$. 求用材料中的方法求出满足条件 $D$ 点坐标.

在平面直角坐标系中, 抛物线 $y=a x^2+b x-3$ 与 $x$ 轴交于点 $A(-1,0)$ 和点 $B(3,0)$, 与 $y$ 轴交于点 $C$.
(1) 求抛物线的解析式及顶点坐标;
( 2 ) 若点 $P$ 为第四象限内抛物线上一点, 当 $\triangle P B C$ 面积最大时, 求点 $P$ 的坐标;
(3) 若点 $P$ 为抛物线上一点, 点 $Q$ 是线段 $B C$ 上一点 (点 $Q$ 不与两端点重合), 是否存在以 $P 、 Q 、 O$ 为顶点的三角形是等腰直角三角形, 若存在, 请直接写出满足条件的点 $P$ 的坐标；若不存在, 请说明理由.

如图, 抛物线 $y=a x^2+b x+3$ 与 $x$ 轴相交于点 $A$, 点 $B$ ( $A$ 在 $B$ 的左侧 ), 与 $y$ 轴相交于点 $C, A$ 、 $B$ 的坐标分别为: $(-2,0) 、(4,0)$, 连接 $A C, B C$.
(1) 求抛物线的解析式；
( 2 ) 如图 1 , 点 $P$ 是第一象限内抛物线上的动点, 过点 $P$ 作 $P E \| y$ 轴, 交直线 $B C$ 于点 $E$, 当 $P E-\frac{4}{5} C E$ 有最大值时, 求 $P E-\frac{4}{5} C E$ 的最大值与点 $P$ 的坐标;
( 3 ) 将抛物线向右平移 2 个单位得到新抛物线 $y^{\prime}$, 点 $F$ 为原抛物线 $y$ 与新抛物线 $y^{\prime}$ 的交点, 点 $M$ 是原抛物线 $y$ 上一点, 当 $\angle M B A=\angle F$ $A B$ 时, 直接写出点 $M$ 的坐标.

我们知道, 二次函数的图像是抛物线, 它也可以这样定义: 若一个动点 $M(x, y)$ 到定点 $A\left(0, \frac{p}{2}\right)$的距离与它到定直线 $y=-\frac{p}{2}$ 的距离相等, 则动点 $M$ 形成的图形就叫抛物线 $x^2=2 p y(p>0)$.
(1) 已知动点 $M(x, y)$ 到定点 $A(0,4)$ 的距离与到定直线 $y=-4$ 的距离相等, 请写出动点 $M$形成的抛物线的解析式.
(2) 若点 $D$ 的坐标是 $(1,8)$, 在 (1) 中求得的抛物线上是否存在点 $P$, 使得 $P A+P D$ 最短?若存在, 求出点 $P$ 的坐标, 若不存在, 请说明理由.

如图, 已知抛物线 $y=a x^2+b x+5$ 经过 $A(-5,0), B(-4,-3)$ 两点, 与 $x$ 轴的另一个交点为 $C$.
(1) 求该抛物线的表达式;
(2) 点 $P$ 为该抛物线上一动点 (与点 $B 、 C$ 不重合), 设点 $P$ 的横坐标为 $m$. 当点 $P$ 在直线 $B C$ 的下方运动时, 求 $\triangle P B C$ 的面积的最大值.

在平面直角坐标系中, 将二次函数 $y=a x^2(a>0)$ 的图像向右平移 1 个单位, 再向下平移 2 个单位, 得到如图所示的抛物线, 该抛物线与 $x$ 轴交于点 $A 、 B$ (点 $A$ 在点 $B$ 的左侧), $O A=1$, 经过点 $A$ 的一次函数 $y=k x+b(k \neq 0)$ 的图像与 $y$ 轴正半轴交于点 $C$, 且与抛物线的另一个交点为 $D, \triangle A B D$ 的面积为 5 .
(1) 求抛物线和一次函数的解析式;
(2) 抛物线上的动点 $E$ 在一次函数的图像下方, 求 $\triangle A C E$ 面积的最大值, 并求出此时点 $E$的坐标.