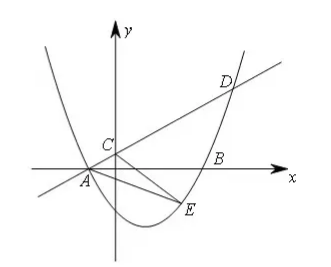
在平面直角坐标系中, 将二次函数 $y=a x^2(a>0)$ 的图像向右平移 1 个单位, 再向下平移 2 个单位, 得到如图所示的抛物线, 该抛物线与 $x$ 轴交于点 $A 、 B$ (点 $A$ 在点 $B$ 的左侧), $O A=1$, 经过点 $A$ 的一次函数 $y=k x+b(k \neq 0)$ 的图像与 $y$ 轴正半轴交于点 $C$, 且与抛物线的另一个交点为 $D, \triangle A B D$ 的面积为 5 .
(1) 求抛物线和一次函数的解析式;
(2) 抛物线上的动点 $E$ 在一次函数的图像下方, 求 $\triangle A C E$ 面积的最大值, 并求出此时点 $E$的坐标.