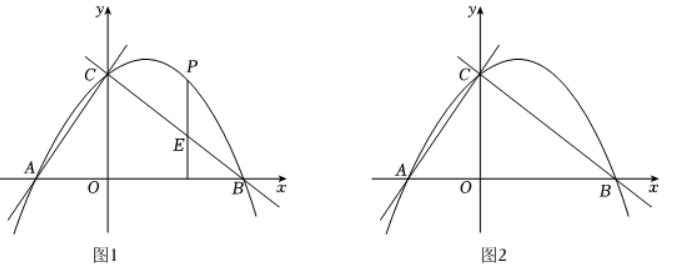
如图, 抛物线 $y=a x^2+b x+3$ 与 $x$ 轴相交于点 $A$, 点 $B$ ( $A$ 在 $B$ 的左侧 ), 与 $y$ 轴相交于点 $C, A$ 、 $B$ 的坐标分别为: $(-2,0) 、(4,0)$, 连接 $A C, B C$.
(1) 求抛物线的解析式;
( 2 ) 如图 1 , 点 $P$ 是第一象限内抛物线上的动点, 过点 $P$ 作 $P E \| y$ 轴, 交直线 $B C$ 于点 $E$, 当 $P E-\frac{4}{5} C E$ 有最大值时, 求 $P E-\frac{4}{5} C E$ 的最大值与点 $P$ 的坐标;
( 3 ) 将抛物线向右平移 2 个单位得到新抛物线 $y^{\prime}$, 点 $F$ 为原抛物线 $y$ 与新抛物线 $y^{\prime}$ 的交点, 点 $M$ 是原抛物线 $y$ 上一点, 当 $\angle M B A=\angle F$ $A B$ 时, 直接写出点 $M$ 的坐标.
(1) 求抛物线的解析式;
( 2 ) 如图 1 , 点 $P$ 是第一象限内抛物线上的动点, 过点 $P$ 作 $P E \| y$ 轴, 交直线 $B C$ 于点 $E$, 当 $P E-\frac{4}{5} C E$ 有最大值时, 求 $P E-\frac{4}{5} C E$ 的最大值与点 $P$ 的坐标;
( 3 ) 将抛物线向右平移 2 个单位得到新抛物线 $y^{\prime}$, 点 $F$ 为原抛物线 $y$ 与新抛物线 $y^{\prime}$ 的交点, 点 $M$ 是原抛物线 $y$ 上一点, 当 $\angle M B A=\angle F$ $A B$ 时, 直接写出点 $M$ 的坐标.
