一、单选题 (共 8 题 ),每题只有一个选项正确
1. 已知集合 , 则
2. 复数 的虚部为
8
-8
3. 已知向量 , 若向量 在向量 上的投影向量为 , 则
2
-2
4. 在 中, , 是 的
充分而不必要条件
必要而不充分条件
充分必要条件
既不充分也不必要条件
5. 过点 与圆 相切的两条直线的夹角为 , 则
6. 五人站成一排, 如果 必须相邻, 那么排法种数为
24
120
48
60
7. 若系列椭圆 的离心率 , 则
8. 已知等差数列 (公差不为 0 ) 和等差数列 的前 项和分别为 , 如果关于 的实系数方程 有实数解, 那么以下 1003 个方程 中, 有实数解的方程至少有 个
499
500
501
502
二、多选题 (共 3 题 ),每题有多个选项正确
9. 已知一组数据: , 若去掉 12 和 45 , 则剩下的数据与原数据相比, 下列结论正确的是
中位数不变
平均数不变
方差不变
第 40 百分位数不变
10. 双曲线
, 左、右顶点分别为
为坐标原点, 如图, 已知动直线
与双曲线
左、右两支分别交于
两点, 与其两条渐近线分别交于
两点, 则下列命题正确的是
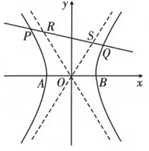
存在直线 , 使得
在运动的过程中, 始终有
若直线 的方程为 , 存在 , 使得 取到最大值
若直线 的方程为 , 则双曲线 的离心率为
11. 如图所示, 有一个棱长为 4 的正四面体
容器,
是
的中点,
是
上的动点, 则下列说法正确的是
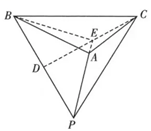
直线 与 所成的角为
的周长最小值为
如果在这个容器中放入 1 个小球 (全部进入), 则小球半径的最大值为
如果在这个容器中放入 4 个完全相同的小球(全部进入), 则小球半径的最大值为
三、填空题 (共 8 题 ),请把答案直接填写在答题纸上
12. 小于 300 的所有末尾是 1 的三位数的和等于
13. 已知函数 , 若 恒成立, 则
14. 已知抛物线 , 点 为抛物线上的动点, 点 与点 的距离 的最小值为 2 ,则
15. 在 中, 的对边分别为 , 已知 .
(1) 求 ;
(2) 已知点 在线段 上, 且 , 求 长.
16. 甲、乙两人进行射击比赛, 每次比赛中, 甲、乙各射击一次, 甲、乙每次至少射中 8 环.根据统计资料可知, 甲击中 8 环、 9 环、 10 环的概率分别为 , 乙击中 8 环、 9 环、 10 环的概率分别为 ,且甲、乙两人射击相互独立.
(1) 在一场比赛中, 求乙击中的环数少于甲击中的环数的概率;
(2) 若独立进行三场比赛, 其中 场比赛中甲击中的环数多于乙击中的环数, 求 的分布列与数学期望.
17. 如图, 圆台
的轴截面为等腰梯形
为底面圆周上异于
的点.

(1) 在平面
内, 过
作一条直线与平面
平行, 并说明理由.
(2) 设平面
平面
与平面
所成角为
, 当四棱椎
的体积最大时, 求
的取值范围.
18. 已知函数 .
(1) 当 时, 探究 零点的个数;
(2) 当 时, 证明: .
19. 阿波罗尼斯是古希腊著名数学家, 他的主要研究成果集中在他的代表作《圆椎曲线》一书中. 阿波罗尼斯圆是他的研究成果之一, 指的是已知动点
与两定点
的距离之比
是一个常数, 那么动点
的轨迹就是阿波罗尼斯圆,圆心在直线
上. 已知动点
的轨迹是阿波罗尼斯圆,其方程为
,定点分别为椭圆
的右焦点
与右顶点
, 且椭圆
的离心率为
.
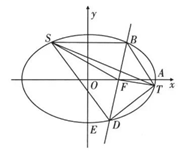
(1) 求椭圆
的标准方程;
(2) 如图, 过右焦点
斜率为
的直线
与椭圆
相交于
(点
在
轴上方), 点
是椭圆
上异于
的两点,
平分
平分
.
①求
的取值范围;
②将点
、、 看作一个阿波罗尼斯圆上的三点, 若
外接圆的面积为
, 求直线
的方程.