阿波罗尼斯是古希腊著名数学家, 他的主要研究成果集中在他的代表作《圆椎曲线》一书中. 阿波罗尼斯圆是他的研究成果之一, 指的是已知动点 $M$ 与两定点 $Q, P$ 的距离之比 $\frac{|M Q|}{|M P|}=\lambda(\lambda>0, \lambda \neq 1), \lambda$ 是一个常数, 那么动点 $M$ 的轨迹就是阿波罗尼斯圆，圆心在直线 $P Q$ 上. 已知动点 $M$ 的轨迹是阿波罗尼斯圆，其方程为 $x^2+y^2=4$,定点分别为椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的右焦点 $F$ 与右顶点 $A$, 且椭圆 $C$ 的离心率为 $e=\frac{1}{2}$.

(1) 求椭圆 $C$ 的标准方程;
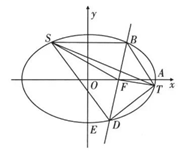
(2) 如图, 过右焦点 $F$ 斜率为 $k(k>0)$ 的直线 $l$ 与椭圆 $C$ 相交于 $B, D$ (点 $B$ 在 $x$ 轴上方), 点 $S, T$ 是椭圆 $C$ 上异于 $B, D$ 的两点, $S F$ 平分 $\angle B S D, T F$ 平分 $\angle B T D$.
①求 $\frac{|B S|}{|D S|}$ 的取值范围;
②将点 $S 、 F 、 T$ 看作一个阿波罗尼斯圆上的三点, 若 $\triangle S F T$ 外接圆的面积为 $\frac{81 \pi}{8}$, 求直线 $l$ 的方程.