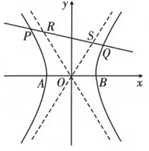
双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$, 左、右顶点分别为 $A, B, O$ 为坐标原点, 如图, 已知动直线 $l$ 与双曲线 $C$ 左、右两支分别交于 $P, Q$ 两点, 与其两条渐近线分别交于 $R, S$ 两点, 则下列命题正确的是

A. 存在直线 $l$, 使得 $A P \| O R$
B. $l$ 在运动的过程中, 始终有 $|P R|=|S Q|$
C. 若直线 $l$ 的方程为 $y=k x+2$, 存在 $k$, 使得 $S_{\triangle O R B}$ 取到最大值
D. 若直线 $l$ 的方程为 $y=-\frac{\sqrt{2}}{2}(x-a), \overrightarrow{R S}=2 \overrightarrow{S B}$, 则双曲线 $C$ 的离心率为 $\sqrt{3}$