单选题 (共 16 题 ),每题只有一个选项正确
$-2021$ 的绝对值是
$\text{A.}$ $2021$
$\text{B.}$ $-2021$
$\text{C.}$ $\frac{1}{2021}$
$\text{D.}$ $-\frac{1}{2021}$
“冠状病毒”是一个大型病毒家族, 科学家借助电子显微镜研究发现, 某冠状病毒的直径约为 0.00000012 米, 0.00000012 用科学记数法表示为
$\text{A.}$ $1.2 \times 10^{-6}$
$\text{B.}$ $1.2 \times 10^{-7}$
$\text{C.}$ $1.2 \times 10^{-8}$
$\text{D.}$ $1.2 \times 10^{-9}$
下列运算正确的是
$\text{A.}$ $\sqrt{(-7)^2}=-7$
$\text{B.}$ $6 \div \frac{2}{3}=9$
$\text{C.}$ $2 a+2 b=2 a b$
$\text{D.}$ $2 a \cdot 3 b=5 a b$
$\sqrt{6} \times \sqrt{\frac{1}{2}}$ 的计算结果估计在
$\text{A.}$ 1 至 1.5 之间
$\text{B.}$ 1.5 至 2 之间
$\text{C.}$ 2 至 2.5 之间
$\text{D.}$ 2.5 至 3 之间
若代数式 $\frac{2}{x-3}$ 有意义, 则实数 $x$ 的取值范围是
$\text{A.}$ $x=0$
$\text{B.}$ $x=3$
$\text{C.}$ $x \neq 0$
$\text{D.}$ $x \neq 3$
若 $a>b$, 则下列不等式中, 错误的是
$\text{A.}$ $3 a>3 b$
$\text{B.}$ $-\frac{a}{3} < -\frac{b}{3}$
$\text{C.}$ $4 a-3>4 b-3$
$\text{D.}$ $a c^2>b c^2$
如图, 有公共顶点 $O$ 的两个边长为 4 的正五边形 (不重叠), 以点 $O$ 为圆心, 4 为半径作弧, 构成一个“蘑萜”形图案(阴影部分), 则这个“蘑菇”形图案的面积为
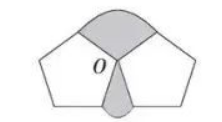
$\text{A.}$ $\frac{24}{5} \pi$
$\text{B.}$ $\frac{28}{5} \pi$
$\text{C.}$ $\frac{32}{5} \pi$
$\text{D.}$ $\frac{36}{5} \pi$
如图, 在 $\triangle A B C$ 中, $D$ 点在 $B C$ 上, 将 $D$ 点分别以 $A B, A C$ 为对称轴, 画出对称点 $E, F$, 并连接 $A E, A F$, 根据图中标示的角度, $\angle E A F$ 的度数为

$\text{A.}$ $120^{\circ}$
$\text{B.}$ $118^{\circ}$
$\text{C.}$ $116^{\circ}$
$\text{D.}$ $114^{\circ}$
在盒子里放有三张分别写有整式 $a+1, a+2,2$ 的卡片, 从中随机抽取两张卡片, 把两张卡片 上的整式分别作为分子和分母,则能组成分式的概率是
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{1}{6}$
$\text{D.}$ $\frac{3}{4}$
若 $967 \times 85=p$, 则 $967 \times 84$ 的值可表示为
$\text{A.}$ $p-1$
$\text{B.}$ $p-85$
$\text{C.}$ $p-967$
$\text{D.}$ $\frac{85}{84} p$
如图, 以 $C D$ 为直径的 $\odot O$ 中, 弦 $A B \perp C D$ 于 $M, A B=16, C M=16$, 则 $M D$ 的长为
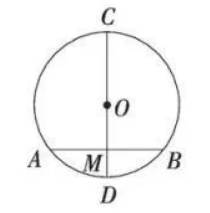
$\text{A.}$ 4
$\text{B.}$ 6
$\text{C.}$ 8
$\text{D.}$ 10
凸透镜成像的原理如图所示, $A D / / l / / B C$, 若物体到焦点的距离 $H F_1$ 与焦点到凸透镜中 心线 $D B$ 的距离 $O F_1$ 之比为 $5: 4$, 则物体被缩小到原来的
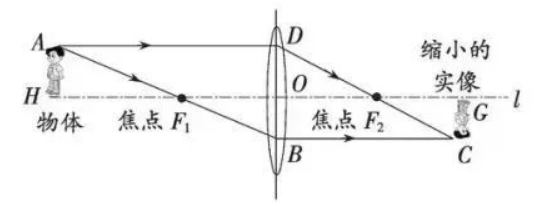
$\text{A.}$ $\frac{4}{5}$
$\text{B.}$ $\frac{2}{5}$
$\text{C.}$ $\frac{4}{9}$
$\text{D.}$ $\frac{5}{9}$
如图, 在 $\triangle A B C$ 中, $A B=8, A C=6, O$ 为 $\triangle A B C$ 的内心, 若 $\triangle A B O$ 的面积为 20 , 则 $\triangle A C O$ 的 面积为
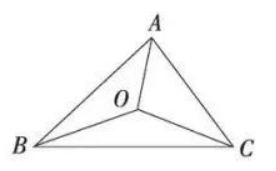
$\text{A.}$ 20
$\text{B.}$ 15
$\text{C.}$ 18
$\text{D.}$ 12
如图, 在平面直角坐标系中, 点 $P\left(-\frac{1}{2}, a\right)$ 在直线 $y=2 x+2$ 与直线 $y=2 x+4$ 之间, 则 $a$ 的取 值范围是
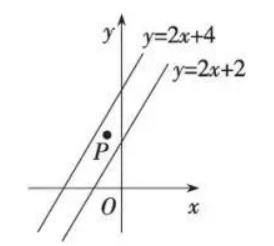
$\text{A.}$ $2 < a < 4$
$\text{B.}$ $1 < a < 3$
$\text{C.}$ $1 < a < 2$
$\text{D.}$ $0 < a < 2$
如图, 已知钝角三角形 $A B C$, 依下列步骤尺规作图,并保留作图痕迹.
步骤 1:以 $C$ 为圆心, $C A$ 为半径画弧(1);
步骤 2:以 $B$ 为圆心, $B A$ 为半径画弧(2), 交弧(1)于点 $D$;
步骤 3: 连接 $A D$, 交 $B C$ 延长线于点 $H$.
下列叙述正确的是

$\text{A.}$ $B H$ 垂直平分线段 $A D$
$\text{B.}$ $A C$ 平分 $\angle B A D$
$\text{C.}$ $S_{\triangle A C}=B C \cdot A H$
$\text{D.}$ $A B=A D$
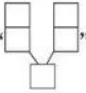
在一平面内, 线段 $A B=8$, 线段 $B C=C D=D A=4$, 将四条线段首尾顺次相接, 把 $A B$ 固定, 当 $A D$ 绕点 $A$ 从 $A B$ 开始逆时针旋转到某一位置时, $B C, C D$ 将 会跟随出现到相应的位置 (如图), 取线段 $C D$ 的中点 $M$, 转 动过程中点 $M$ 与点 $B$ 距离不可能是
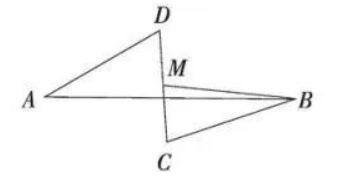
$\text{A.}$ 3
$\text{B.}$ 5
$\text{C.}$ 6
$\text{D.}$ 8
填空题 (共 4 题 ),请把答案直接填写在答题纸上
设 $x_1, x_2$ 是一元二次方程 $x^2-x-1=0$ 的两根, 则 $x_1+x_2+x_1 x_2=$
如图, 已知矩形 $A B C D, P, R$ 分别是 $B C$ 和 $D C$ 上的点, $E, F$ 分别是 $P A, P R$ 的中点, 如果 $D R=3, A D=4$, 则 $E F$ 的长为
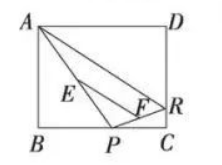
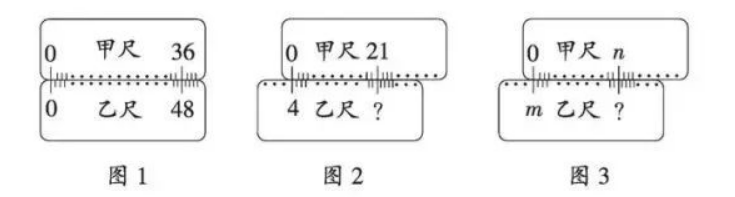
如图 1 所示, 已知甲、乙为两把不同刻度的直尺, 且同一把直尺上的刻度之间距离相等, 小研将此两把直尺紧贴, 并将两直尺上的刻度 0 彼此对准后, 发现甲尺的刻度 36 会对准 乙尺的刻度 48 .
(1)如图 2, 若将甲尺向右平移且平移过程中两把直尺维持紧贴, 使得甲尺的刻度 0 对准乙 尺的刻度 4 , 则此时甲尺的刻度 21 会对准乙尺的刻度是
(2)如图 3, 若将甲尺向右平移且平移过程中两把直尺维持紧贴, 使得甲尺的刻度 0 会对准 乙尺的刻度 $m$, 如图 3 所示, 则此时甲尺的刻度 $n$ 会对准乙尺的刻度是 . 用含 $m, n$ 的式子表示)
用直尺画数轴时, 数轴上的点 $A, B, C$ 分别代表数字 $a, b, c$, 已知 $A B=6, B C=2$, 如图 所示.设点 $p=a+b+c$, 该数轴的原点为 $O$.
(1) 若点 $A$ 所表示的数是 -1 , 则点 $C$ 所表示的数是 ________
(2) 若点 $A, B$ 所表示的数互为相反数, 则点 $C$ 所表示的数是 ________ , 此时 $p$ 的值为 ________
(3)若数轴上点 $C$ 表示的数为 4 , 求 $p$ 的值.

解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
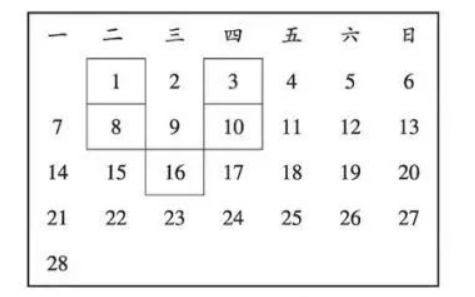
如图是 2022 年 2 月的日历表:
(1)在图中用优美的
$\mathrm{U}$ 形框框住五个数, 其中最小的数为 1 , 则 $\mathrm{U}$ 形框中的五个数
字之和为
(2)在图中将 $\mathrm{U}$ 形框上下左右移动, 框住日历表中的 5 个数字, 设最小的数字为 $x$, 用代数 式表示 $U$ 形框框住的五个数字之和为
(3) 在图中移动 $U$ 形框的位置, 框住的五个数字之和可以为 63 吗? 若能, 求出这五个数字 中最小的数; 若不能, 请说明理由.
如图 $1, A, B, C$ 是郑州市二七区三个垃圾存放点, 点 $B, C$ 分别位于点 $A$ 的正北和 正东方向, $A B=60$ 米, 6 位环卫工人分别测得的 $B C$ 长度如下表:

他们又调查了各点的垃圾量, 并绘制了下列不完整的统计图 2 .
(1)表中的中位数是 ,众数是 ,$B C$ 长度的平均数 $\bar{x}=$
(2)求 $A$ 处的垃圾量,并将图 2 补充完整;
(3) 用 (1) 中的 $\bar{x}$ 作为 $B C$ 的长度, 要将 $A$ 处的垃圾沿道路 $A C$ 都运到 $C$ 处, 已知运送 1 千 克垃圾每米的费用为 0.05 元, 求运垃圾所需的费用.

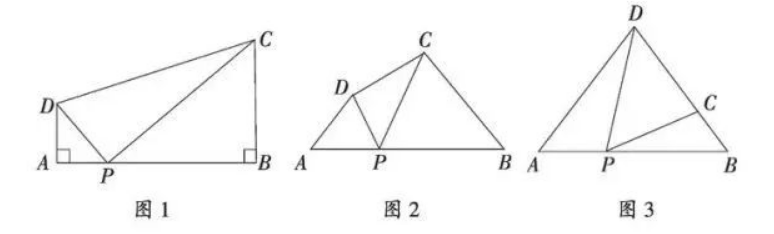
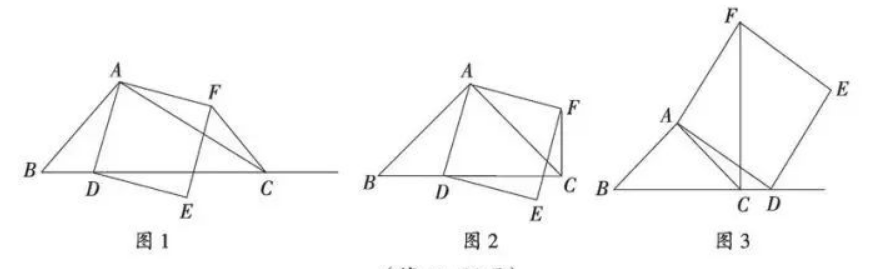
如图 1, 在 $\triangle A B C$ 中, $\angle A C B$ 为锐角, 点 $D$ 为射线 $B C$ 上一点, 连接 $A D$, 以 $A D$ 为 一边且在 $A D$ 的右侧作正方形 $A D E F$, 连接 $C F$.
(1) 如果 $A B=A C, \angle B A C=90^{\circ}$.
①当点 $D$ 在线段 $B C$ 上时 (与点 $B$ 不重合), 如图 2 , 线段 $C F, B D$ 所在直线的位置关系为 ________ , 线段 $C F, B D$ 的数量关系为 ________
②当点 $D$ 在线段 $B C$ 的延长线上时, 如图 3,(1)中的结论是否仍然成立, 并说明理由;
(2) 如果 $A B \neq A C, \angle B A C$ 是锐角, 点 $D$ 在线段 $B C$ 上, 当 $\angle A C B$ 满足什么条件时, $C F \perp B C$ (点 $C, F$ 不重合), 请直接写出答案.
某设计师结合数学知识设计一款沙发, 沙发三视图如图 1 所示, 将沙发侧面展示 图简化后, 得到图 2 所示图形. 为了解沙发相关性能, 设计师将图形放人平面直角坐标系, 其中曲线 $A B$ 是反比例函数 $y=\frac{k}{x}(k \neq 0)$ 的一段图象, 线段 $B D$ 是一次函数 $y=\frac{1}{5} x+b$ 的一 段图像,点 $B(20,32)$, 沙发腿 $D E \perp x$ 轴,请你根据图形解决以下问题:
(1) 请求出反比例函数表达式和一次函数表达式 (不要求写 $x$ 的取值范围);
(2) 过点 $A$ 向 $x$ 轴作垂线, 交 $x$ 轴于点 $F$, 已知 $C F=4 \mathrm{~cm}, D E=40 \mathrm{~cm}, \tan \alpha=4$, 设计师想用一 个长方体箱子将沙发放进去, 则这个长方体箱子长、宽、高至少分别是多少?

将小球 (看作一点)以速度 $v_1$ 坚直上抛, 上升速度随时间推移逐渐减少直至为 0 , 此时小球达到最大高度, 小球相对于抛出点的高度 $y(\mathrm{~m})$ 与时间 $t(\mathrm{~s})$ 的函数解析式为两部 分之和, 其中一部分为速度 $v_1(\mathrm{~m} / \mathrm{s})$ 与时间 $t(\mathrm{~s})$ 的积, 另一部分与时间 $t(\mathrm{~s})$ 的平方成正比. 若上升的初始速度 $v_1=10 \mathrm{~m} / \mathrm{s}$, 且当 $t=1 \mathrm{~s}$ 时, 小球达到最大高度.
(1)求小球上升的高度 $y$ 与时间 $t$ 的函数关系式 (不必写范围), 并写出小球上升的最大 高度;
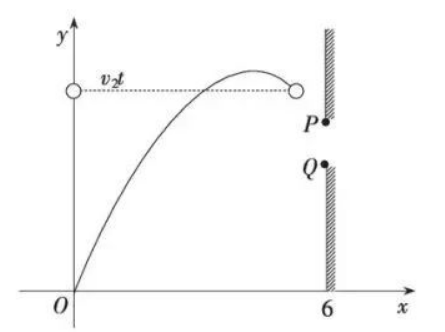
(2)如图, 平面直角坐标系中, $y$ 轴表示小球相对于抛出点的高度, $x$ 轴表示小球距抛出点的 水平距离, 向上抛出小球时再给小球一个水平向前的均匀速度 $v_2(\mathrm{~m} / \mathrm{s})$, 发现小球运动的路 线为一抛物线, 其相对于抛出点的高度 $y(\mathrm{~m})$ 与时间 $t(\mathrm{~s})$ 的函数解析式与 (1) 中的解析式相同.
(1)若 $v_2=5 \mathrm{~m} / \mathrm{s}$, 当 $t=\frac{3}{2} \mathrm{~s}$ 时,小球的坐标为 , 小球上升的最高点坐标为 ;求小 球上升的高度 $y$ 与小球距抛出点的水平距离 $x$ 之间的函数关系式;
(2)在小球的正前方的墙上有一高 $\frac{35}{36} \mathrm{~m}$ 的小窗户 $P Q$, 其上沿 $P$ 的坐标为 $\left(6, \frac{15}{4}\right)$, 若小球 恰好能从窗户中穿过 (不包括恰好击中点 $P, Q$, 墙厚度不计), 请直接写出小球的水平速度 $v_2$ 的取值范围.
问题背景: 如图 1, 在四边形 $A B C D$ 中, 点 $P$ 为 $A B$ 上一点, $\angle D P C=\angle A=\angle B=90^{\circ}$, 求证: $A D \cdot B C=A P \cdot B P$. (无需证明)
(1)探究:
如图 2, 在四边形 $A B C D$ 中, 点 $P$ 为 $A B$ 上一点, 当 $\angle D P C=\angle A=\angle B=\theta$ 时, 上述结论是否依 然成立? 说明理由;
(2)应用:
请利用(1) 获得的经验解决问题:
如图 3, 在 $\triangle A B D$ 中, $A B=6, A D=B D=5$, 点 $P$ 以每秒 1 个单位长度的速度, 由点 $A$ 出发, 沿 边 $A B$ 向点 $B$ 运动, 且满足 $\angle D P C=\angle A$, 设点 $P$ 的运动时间为 $t$ (秒), 当以 $D$ 为圆心, 以 $D C$ 为半径的圆与 $A B$ 相切时, 求 $t$ 的值;
(3)拓展 :
在(2) 的条件下, 当 $0 \leqslant t \leqslant 4$ 时, 直接写出点 $C$ 在边 $B D$ 上所走的总路程 $d=$