将小球 (看作一点)以速度 $v_1$ 坚直上抛, 上升速度随时间推移逐渐减少直至为 0 , 此时小球达到最大高度, 小球相对于抛出点的高度 $y(\mathrm{~m})$ 与时间 $t(\mathrm{~s})$ 的函数解析式为两部 分之和, 其中一部分为速度 $v_1(\mathrm{~m} / \mathrm{s})$ 与时间 $t(\mathrm{~s})$ 的积, 另一部分与时间 $t(\mathrm{~s})$ 的平方成正比. 若上升的初始速度 $v_1=10 \mathrm{~m} / \mathrm{s}$, 且当 $t=1 \mathrm{~s}$ 时, 小球达到最大高度.
(1)求小球上升的高度 $y$ 与时间 $t$ 的函数关系式 (不必写范围), 并写出小球上升的最大 高度;
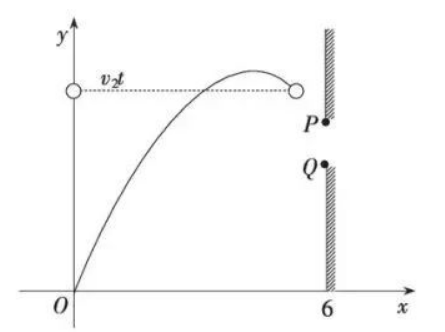
(2)如图, 平面直角坐标系中, $y$ 轴表示小球相对于抛出点的高度, $x$ 轴表示小球距抛出点的 水平距离, 向上抛出小球时再给小球一个水平向前的均匀速度 $v_2(\mathrm{~m} / \mathrm{s})$, 发现小球运动的路 线为一抛物线, 其相对于抛出点的高度 $y(\mathrm{~m})$ 与时间 $t(\mathrm{~s})$ 的函数解析式与 (1) 中的解析式相同.
(1)若 $v_2=5 \mathrm{~m} / \mathrm{s}$, 当 $t=\frac{3}{2} \mathrm{~s}$ 时,小球的坐标为 , 小球上升的最高点坐标为 ;求小 球上升的高度 $y$ 与小球距抛出点的水平距离 $x$ 之间的函数关系式;
(2)在小球的正前方的墙上有一高 $\frac{35}{36} \mathrm{~m}$ 的小窗户 $P Q$, 其上沿 $P$ 的坐标为 $\left(6, \frac{15}{4}\right)$, 若小球 恰好能从窗户中穿过 (不包括恰好击中点 $P, Q$, 墙厚度不计), 请直接写出小球的水平速度 $v_2$ 的取值范围.
(1)求小球上升的高度 $y$ 与时间 $t$ 的函数关系式 (不必写范围), 并写出小球上升的最大 高度;
(2)如图, 平面直角坐标系中, $y$ 轴表示小球相对于抛出点的高度, $x$ 轴表示小球距抛出点的 水平距离, 向上抛出小球时再给小球一个水平向前的均匀速度 $v_2(\mathrm{~m} / \mathrm{s})$, 发现小球运动的路 线为一抛物线, 其相对于抛出点的高度 $y(\mathrm{~m})$ 与时间 $t(\mathrm{~s})$ 的函数解析式与 (1) 中的解析式相同.
(1)若 $v_2=5 \mathrm{~m} / \mathrm{s}$, 当 $t=\frac{3}{2} \mathrm{~s}$ 时,小球的坐标为 , 小球上升的最高点坐标为 ;求小 球上升的高度 $y$ 与小球距抛出点的水平距离 $x$ 之间的函数关系式;
(2)在小球的正前方的墙上有一高 $\frac{35}{36} \mathrm{~m}$ 的小窗户 $P Q$, 其上沿 $P$ 的坐标为 $\left(6, \frac{15}{4}\right)$, 若小球 恰好能从窗户中穿过 (不包括恰好击中点 $P, Q$, 墙厚度不计), 请直接写出小球的水平速度 $v_2$ 的取值范围.
