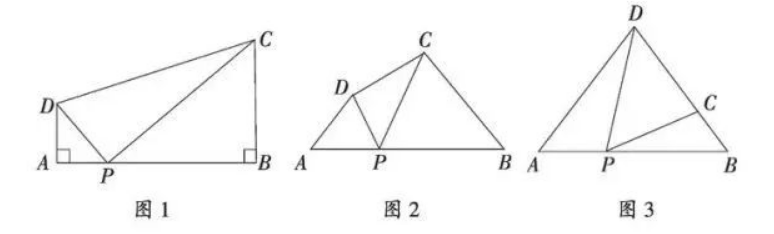
问题背景: 如图 1, 在四边形 $A B C D$ 中, 点 $P$ 为 $A B$ 上一点, $\angle D P C=\angle A=\angle B=90^{\circ}$, 求证: $A D \cdot B C=A P \cdot B P$. (无需证明)
(1)探究:
如图 2, 在四边形 $A B C D$ 中, 点 $P$ 为 $A B$ 上一点, 当 $\angle D P C=\angle A=\angle B=\theta$ 时, 上述结论是否依 然成立? 说明理由;
(2)应用:
请利用(1) 获得的经验解决问题:
如图 3, 在 $\triangle A B D$ 中, $A B=6, A D=B D=5$, 点 $P$ 以每秒 1 个单位长度的速度, 由点 $A$ 出发, 沿 边 $A B$ 向点 $B$ 运动, 且满足 $\angle D P C=\angle A$, 设点 $P$ 的运动时间为 $t$ (秒), 当以 $D$ 为圆心, 以 $D C$ 为半径的圆与 $A B$ 相切时, 求 $t$ 的值;
(3)拓展 :
在(2) 的条件下, 当 $0 \leqslant t \leqslant 4$ 时, 直接写出点 $C$ 在边 $B D$ 上所走的总路程 $d=$
(1)探究:
如图 2, 在四边形 $A B C D$ 中, 点 $P$ 为 $A B$ 上一点, 当 $\angle D P C=\angle A=\angle B=\theta$ 时, 上述结论是否依 然成立? 说明理由;
(2)应用:
请利用(1) 获得的经验解决问题:
如图 3, 在 $\triangle A B D$ 中, $A B=6, A D=B D=5$, 点 $P$ 以每秒 1 个单位长度的速度, 由点 $A$ 出发, 沿 边 $A B$ 向点 $B$ 运动, 且满足 $\angle D P C=\angle A$, 设点 $P$ 的运动时间为 $t$ (秒), 当以 $D$ 为圆心, 以 $D C$ 为半径的圆与 $A B$ 相切时, 求 $t$ 的值;
(3)拓展 :
在(2) 的条件下, 当 $0 \leqslant t \leqslant 4$ 时, 直接写出点 $C$ 在边 $B D$ 上所走的总路程 $d=$
