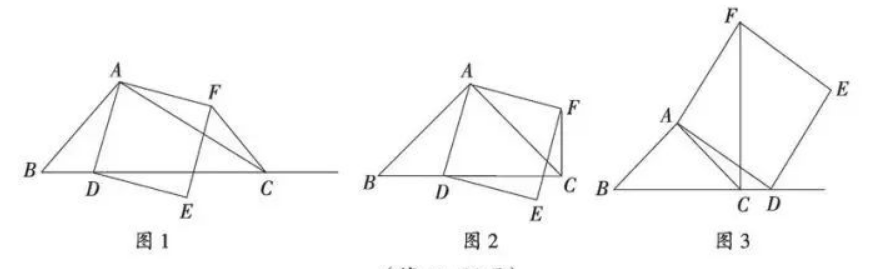
如图 1, 在 $\triangle A B C$ 中, $\angle A C B$ 为锐角, 点 $D$ 为射线 $B C$ 上一点, 连接 $A D$, 以 $A D$ 为 一边且在 $A D$ 的右侧作正方形 $A D E F$, 连接 $C F$.
(1) 如果 $A B=A C, \angle B A C=90^{\circ}$.
①当点 $D$ 在线段 $B C$ 上时 (与点 $B$ 不重合), 如图 2 , 线段 $C F, B D$ 所在直线的位置关系为 ________ , 线段 $C F, B D$ 的数量关系为 ________
②当点 $D$ 在线段 $B C$ 的延长线上时, 如图 3,(1)中的结论是否仍然成立, 并说明理由;
(2) 如果 $A B \neq A C, \angle B A C$ 是锐角, 点 $D$ 在线段 $B C$ 上, 当 $\angle A C B$ 满足什么条件时, $C F \perp B C$ (点 $C, F$ 不重合), 请直接写出答案.