单选题 (共 3 题 ),每题只有一个选项正确
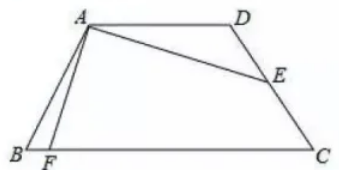
如图, 已知四边形 $A B C D$ 为等腰梯形, $A D / / B C, A B=C D, A D=\sqrt{2}, E$ 为 $C D$ 中点, 连接 $A E$, 且 $A E=2 \sqrt{3}, \angle D A E=30^{\circ}$, 作 $A E \perp A F$ 交 $B C$ 于 $F$, 则 $B F=$
$\text{A.}$ $1$
$\text{B.}$ $3-\sqrt{3}$
$\text{C.}$ $\sqrt{5}-1$
$\text{D.}$ $4-2 \sqrt{2}$
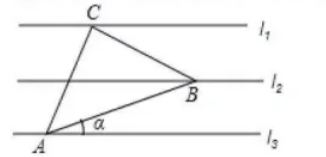
如图, 已知 $I_1 / / I_2 / / I_3$, 相邻两条平行直线间的距离相等, 若等腰直角 $\triangle A B C$ 的三个顶 点分别在这三条平行直线上, 则 $\sin a$ 的值是
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $\frac{6}{17}$
$\text{C.}$ $\frac{\sqrt{5}}{5}$
$\text{D.}$ $\frac{\sqrt{10}}{10}$
如图所示, 点 $P(3 a, a)$ 是反比例函数 $y=\frac{k}{x}(k>0)$ 与 $\odot 0$ 的一个交点, 图中阴影部 分的面积为 $10 \pi$, 则反比例函数的解析式为

$\text{A.}$ $y=\frac{3}{x}$
$\text{B.}$ $y=\frac{5}{x}$
$\text{C.}$ $\mathrm{y}=\frac{10}{\mathrm{x}}$
$\text{D.}$ $y=\frac{12}{x}$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
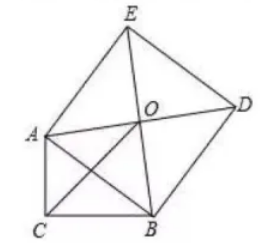
如图, Rt $\triangle A B C$ 中, $\angle C=90^{\circ}$, 以斜边 $A B$ 为边向外作正方形 $A B D E$, 且正方形对角线 交于点 0 , 连接 $O C$, 已知 $A C=5, O C=6 \sqrt{2}$, 则另一直角边 $B C$ 的长为
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
观察以下 10 个乘积,回答下列问题.
$
11 \times 29 ; 12 \times 28 ; 13 \times 27 ; 14 \times 26 ; 15 \times 25 ; 16 \times 24 ; 17 \times 23 ; 18 \times 22 ; 19 \times 21 ; 20 \times 20
$
【探究】经探究发现以上各乘积均可以写成平方差的形式.
例如: $11 \times 29=x^2-y^2=(x+y)(x-y)$, 列出方程组, 解 $x, y$ 的值即可.
按照以上思路写出“将11×29 写成平方差的形式”的完整过程;
【发现】观察以上 10 个乘积,当 $a+b=40$ 时, $a b$ ( ) $20^2$ (比较大小)
【拓展】当 $\mathrm{a}+\mathrm{b}=\mathrm{m}$ 时, 比较 $\mathrm{ab}$ 与 $\left(\frac{\mathrm{m}}{2}\right)^2$ 的大小, 并说明理由.
我们知道: 分式和分数有着很多的相似点. 如类比分数的基本性质, 我们得到了分式的 基本性质, 等等. 小学里, 把分子比分母小的分数叫做真分数. 类似地, 我们把分子的次数 小于分母的次数的分式称为真分式; 反之, 称为假分式. 对于任何一个假分式都可以化成整 式与真分式的和的形式, 如 $\frac{x+1}{x-1}=\frac{x-1+2}{x-1}=\frac{x-1}{x-1}+\frac{2}{x-1}=1+\frac{2}{x-1}$.
(1)下列分式中,属于真分式的是
A. $\frac{x^2}{x-1}$
B. $\frac{x-1}{x+1}$
C. $-\frac{3}{2 x-1}$
D. $\frac{x^2+1}{x^2-1}$
(2) 将假分式 $\frac{m^2+3}{m+1}$ 化成整式和真分式的和的形式.
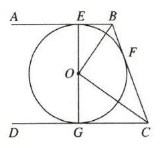
如图 , 已知直线 $A B / / C D$, 过直线 $A B$ 上一点 $E$ 作 $E G \perp C D$ 于 $G$ 点, 以 $E G$ 为直径 作 $\odot O$, 直线 $B C$ 与 $\odot O$ 交于点 $F$, 且 $B E=B F$, 连接 $O B, O C$.
(1) 求证: $B C$ 是 $\odot O$ 的切线;
(2) 若 $\odot O$ 的半径为 3 , 且 $S_{\triangle O B C}=3 \sqrt{10}$, 求 $C G-B E$ 的值.
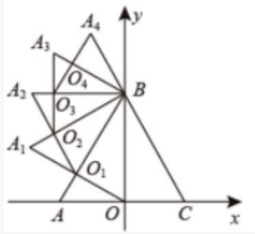
已知二次函数的解析式为 $y=-x^2+4 x$, 该二次函数交 $x$ 轴 于 $O 、 B$ 两点, $A$ 为抛物线上一点, 且横纵坐标相等 (原点除外),
$P$ 为二次函数上一动点, 过 $P$ 作 $x$ 轴垂线, 垂足为 $D(a, 0)(a>0)$, 并与直线 $O A$ 交于点 $C$.
(1)求 $A 、 B$ 两点的坐标;
(2)当点 $P$ 在线段 $O A$ 上方时, 过 $P$ 作 $x$ 轴的平行线与线段 $O A$ 相交于点 $E$, 求 $\triangle P C E$ 周长的最大值及此时 $P$ 点的坐标;
(3)当 $P C=C O$ 时,求 $P$ 点坐标.
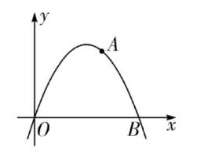
如图, 已知正方形 $A B C D$ 的对角线 $A C, B D$ 相交于点 $M$, 顶点 $\mathrm{A}, B, C$ 的坐标分别 为 $(1,3),(1,1),(3,1)$, 规定“把正方形 $A B C D$ 先沿 $x$ 轴翻折, 再向右平移1个单位"为一次变 换, 如此这样, 连续经过 2020 次变换后, 求点 $M$ 的坐标变。
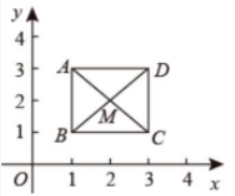
如图, 边长为 4 的等边 $\triangle A B C, A C$ 边在 $x$ 轴上, 点 $B$ 在 $y$ 轴的正半轴上, 以 $O B$ 为边作 等边 $\triangle O B A_1$, 边 $O A_1$ 与 $A B$ 交于点 $O_1$, 以 $O_1 B$ 为边作等边 $\triangle O_1 B A_2$, 边 $O_1 A_2$ 与 $A_1 B$ 交于点 $O_2$, 以 $O_2 B$ 为边作等边 $\triangle O_2 B A_3$, 边 $O_2 A_3$ 与 $A_2 B$ 交于点 $O_3, \mathrm{~L}$, 依此规律连续作等边 $\triangle O_{n-1} B A_n$, 则 $A_{2021}$ 的横坐标为
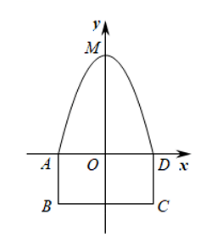
如图, 是一个仓库的横截面, 截面的轮廓可以看成由一个矩 形 $A B C D$ 和抛物线的一部分组成, $A B=2 \mathrm{~m}, A D=4 \mathrm{~m}$, 抛物线的顶点 $M$ 到 $A D$ 的距离 为 $4 \mathrm{~m}$. 为了测算该仓库的储藏空间, 小明以 $A D$ 所在直线为 $x$ 轴, 以拋物线的对称轴为 $y$ 轴, 建立了如图所示的平面直角坐标系, 请继续解决下列问题:
(1) 求该抛物线所对应的函数表达式;
(2) 若存放的货物横截面为正方形, 并使得正方形的一边在 $B C$ 上且面积最大, 求此 正方形的面积;
(3) 若存放的货物横截面为矩形, 并使得矩形的一边在 $B C$ 上且周长最大, 求此矩形 的周长.