如图, 是一个仓库的横截面, 截面的轮廓可以看成由一个矩 形 $A B C D$ 和抛物线的一部分组成, $A B=2 \mathrm{~m}, A D=4 \mathrm{~m}$, 抛物线的顶点 $M$ 到 $A D$ 的距离 为 $4 \mathrm{~m}$. 为了测算该仓库的储藏空间, 小明以 $A D$ 所在直线为 $x$ 轴, 以拋物线的对称轴为 $y$ 轴, 建立了如图所示的平面直角坐标系, 请继续解决下列问题:
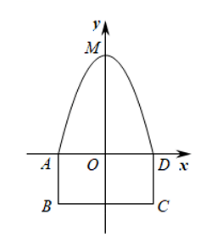
(1) 求该抛物线所对应的函数表达式;
(2) 若存放的货物横截面为正方形, 并使得正方形的一边在 $B C$ 上且面积最大, 求此 正方形的面积;
(3) 若存放的货物横截面为矩形, 并使得矩形的一边在 $B C$ 上且周长最大, 求此矩形 的周长.

(1) 求该抛物线所对应的函数表达式;
(2) 若存放的货物横截面为正方形, 并使得正方形的一边在 $B C$ 上且面积最大, 求此 正方形的面积;
(3) 若存放的货物横截面为矩形, 并使得矩形的一边在 $B C$ 上且周长最大, 求此矩形 的周长.