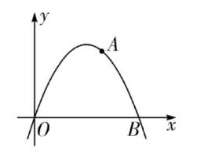
已知二次函数的解析式为 $y=-x^2+4 x$, 该二次函数交 $x$ 轴 于 $O 、 B$ 两点, $A$ 为抛物线上一点, 且横纵坐标相等 (原点除外),
$P$ 为二次函数上一动点, 过 $P$ 作 $x$ 轴垂线, 垂足为 $D(a, 0)(a>0)$, 并与直线 $O A$ 交于点 $C$.
(1)求 $A 、 B$ 两点的坐标;
(2)当点 $P$ 在线段 $O A$ 上方时, 过 $P$ 作 $x$ 轴的平行线与线段 $O A$ 相交于点 $E$, 求 $\triangle P C E$ 周长的最大值及此时 $P$ 点的坐标;
(3)当 $P C=C O$ 时,求 $P$ 点坐标.
$P$ 为二次函数上一动点, 过 $P$ 作 $x$ 轴垂线, 垂足为 $D(a, 0)(a>0)$, 并与直线 $O A$ 交于点 $C$.
(1)求 $A 、 B$ 两点的坐标;
(2)当点 $P$ 在线段 $O A$ 上方时, 过 $P$ 作 $x$ 轴的平行线与线段 $O A$ 相交于点 $E$, 求 $\triangle P C E$ 周长的最大值及此时 $P$ 点的坐标;
(3)当 $P C=C O$ 时,求 $P$ 点坐标.
