单选题 (共 10 题 ),每题只有一个选项正确
-2023 的相反数是
$\text{A.}$ 2023
$\text{B.}$ -2023
$\text{C.}$ $-\frac{1}{2023}$
$\text{D.}$ $\frac{1}{2023}$
2. 下列图形中, 是中心对称图形的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
下列计算不正确的是
$\text{A.}$ $x^2 \cdot x^{-3}=\frac{1}{x}$
$\text{B.}$ $\sqrt[3]{-x^3}=-x$
$\text{C.}$ $\left(-m n^3\right)^2=m^2 n^6$
$\text{D.}$ $2 x^6 \div x^2=2 x^3$
2022 年十三届全国人大五次会议审议通过的政府工作报告中提出, 今年城镇新增就业目标 为 11000000 人以上,数据 1,1000000 用科学记数法表示为
$\text{A.}$ $0.11 \times 10^8$
$\text{B.}$ $11 \times 10^6$
$\text{C.}$ $1.1 \times 10^6$
$\text{D.}$ $1.1 \times 10^7$
将一个矩形纸条按如图所示的方法折叠, 若 $\angle 2=110^{\circ}$, 则 $\angle 1$ 的度数为

$\text{A.}$ $30^{\circ}$
$\text{B.}$ $40^{\circ}$
$\text{C.}$ $50^{\circ}$
$\text{D.}$ $70^{\circ}$
为落实“双减”政策, 我校通过各利丰富的校园活动, 充实课后服务. 某班篮球队有篮球运动员10 人,进行投篮训练,每人投篮 30 个, 投中球数如下表:

在这组数据中, 中位数和众数分别为
$\text{A.}$ 27,29
$\text{B.}$ 28,29
$\text{C.}$ 27,30
$\text{D.}$ 29,29
有五张卡片(除字外完全相同), 正面分别写有“学”“习”“二”“十”“大”, 将这五张卡片反面朝上洗匀后放在桌面上・小朋从中任意抽取两张卡片,抽到的卡片恰好写有“学”“习”的概率是
$\text{A.}$ $\frac{1}{10}$
$\text{B.}$ $\frac{1}{8}$
$\text{C.}$ $\frac{1}{6}$
$\text{D.}$ $\frac{2}{5}$
我国古代著作《增用算法统宗》中记载了一首古算诗: “庭前孩童闹如簇, 不知人数不知梨. 每人四梨多十二.每人六梨恰齐足.”.”设孩童有 $x$ 名,则可列方程为
$\text{A.}$ $4 x-12=6 x$
$\text{B.}$ $4 x+12=6 . x$
$\text{C.}$ $\frac{x}{4}-12=\frac{x}{6}$
$\text{D.}$ $\frac{x}{4}+\frac{x}{6}=12$
随着科技的进步, 我国的生物医药行业发展迅速, 最近某药品研究所开发一种抗菌新药, 首次 用于临床人体试验, 测得成人服药后血液中药物浓度 $y$ (微克/毫升)与服药时间 $x$ (小时)之间 的函数关系如图所示 (当 $3 \leqslant x \leqslant 10$ 时, $y$ 与 $x$ 成反比例). 根据图中信息可知, 血液中药物浓 度不低于 6 微克/毫升的持续时间为
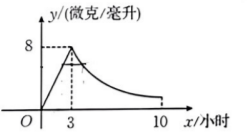
$\text{A.}$ 4 小时
$\text{B.}$ $\frac{9}{4}$ 小时
$\text{C.}$ $\frac{7}{4}$ 小时
$\text{D.}$ $\frac{5}{4}$ 小时
如图. 四边形 $A B C D$ 为正方形, 以 $B$ 为圆心, $B C$ 长为半径画 $A C, P$ 为四边形内部一点, $C P$ $=\sqrt{3}, B P \perp C P, \angle B C P=30^{\circ}$, 连接 $A P$, 则阴影部分的面积为
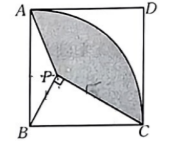
$\text{A.}$ $\pi-\frac{\sqrt{3}}{2}$
$\text{B.}$ $2 \pi-\frac{1}{2}$
$\text{C.}$ $\pi-\frac{\sqrt{3}-1}{2}$
$\text{D.}$ $\pi-\frac{\sqrt{3}+1}{2}$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
$\sqrt{20} \times \sqrt{\frac{1}{5}}=$
如图, 在平面直角坐标系中, 直线 $y=-\frac{4}{3} x+4$ 交坐标轫于 $A, B$ 两点, 若 $P$ 是直线上的一 个动点, 将点 $O$ 绕点 $P$ 逆时针旋转 $90^{\circ}$, 得到点 $C$, 连接 $O C$, 则 $O C$ 的最小值为
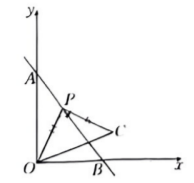
如图, 在菱形 $A B C D$ 中. $E$ 为边 $C D$ 上一点. 过点 $E$ 作 $E F \perp A C$ 于点 $P$, 交 $A B$ 的延长线于 点 $F$, 若 $C E: B F=2: 3$. 则 $C P: A P$ 的值为
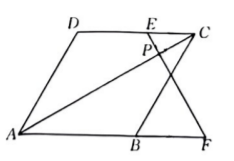
用同样大小的正方体木块依次隹放成如图 1、图 2、图 3 所示的实心儿何体, 并按照这样的规 律继续堆放下去、则图 $n$ 有 个正方体. (用含 $n$ 的式子表示)

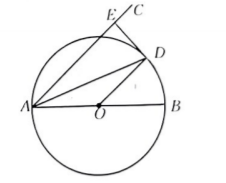
如图, $A B$ 是 $\odot O$ 的直径, 弦 $A D$ 平分 $\angle C A B$, 连接 $O D$, 过点 $D$ 作 $\odot O$ 的切线交 $A C$ 于点 $E$, 若 $\angle C A D=22.5^{\circ}, A B=2 \sqrt{2}$, 则 $D E$ 的长为
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
(1)计算: $\left(-\frac{1}{2}\right)^2 \times|-3+1|-\left(-1+\frac{1}{2}\right)$.
(2) 下面是小琛同学解不等式的过程, 请认真阅读并完成相应任务.
$$
\frac{x-1}{3}-\frac{2 x-1}{2}>1 .
$$
解:
去分母, 得 $2(x-1)-3(2 x-1)>6$, .....第一步
去括号, 得 $2 x-2-6 x+3>6$, ......第二步
移项, 得 $2 x-6 x>6+3-2$, ......第三步
合并同类项, 得 $-4 x>7$, .......第四步
两边都除以 -1 , 得 $x < -\frac{7}{4}$. ......第五步
任务:
(1)上述解题过程中, 第二步是依据 (运算律)进行变形的.
(2)第 ( ) 步开始出现错误, 这一步错误的原因是
(3)请直接写出该不等式的正确解集.
尊老爱幼是中华民族的传统美德, 元旦前夕, 某商场为老人推出一款特价商品, 每件商品的进价 为 15 元, 促销前销售单价为 25 元, 平均每天能售出 80 件. 根据市场调查, 在每件商品盈利不少 于 5 元的前提下,销售单价每降低 0.5 元, 平均每天可多售出 20 件. 若不考虑其他因素的影响, 商店要使销售这款商品的利润平均每天 1280 元, 每件商品的定价应为多少元?
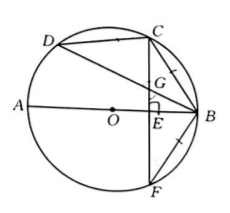
如图, $A B$ 是 $\odot O$ 的直径, $C$ 为 $B D$ 的中点, $C F$ 为 $\odot O$ 的弦, 且 $C F \perp A B$, 垂足为 $E$, 连接 $B D$ 交 $C F$ 于点 $G$, 连接 $C D, B C, B F$. 求证: $D G=G F$.
2022年10月12日.“天宫课堂”第三课开诽, 神舱十四号乘纠航天员陈冬、刘洋、蔡旭哲在中国空间站演示了微重力环境下毛细效应A、水球变懒B、太空趣味饮水C和会调头的扳手D 四个精彩试验, 为了解本次“太空科普知识”掌握情况, 某校随机抽取部分学生作问卷调查, 并进行了测试, 整理后得到统计图和统计表如下.
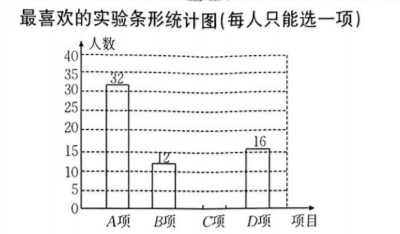
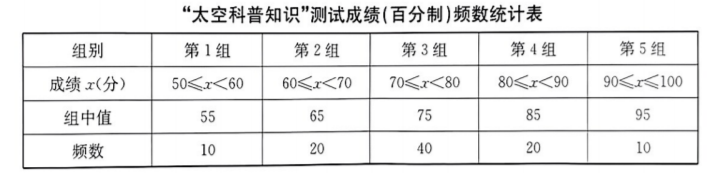
根据以上信息, 回答下列问题:
(1)这次调查的样本容量是 ,并补全条形统计图.
(2) 在这次测试中,成绩的中位数在第 组,成绩不低于 80 分的人数占测试人数的百分比 为
(3)估计本次测试的平均数, 并对该校学生 “太空科普知识”的掌握情况作出合理的评价 (写出一 条即可).
《见微知著》写道: 从一个简单的经典问题出发, 从特殊到一般, 由简单到复杂; 从部分到整体, 由低维到高维. 知识与方法的类比是探索发展的重要途径,是发现新问题、新结论的重要方法.
阅读材料一: 利用整体思想、代数式的恒等变形解题, 使不少依照常规思路难以解决的问题找到简便的解决方法,常用途径: (1)整体观察; (2) 整体设元; (3) 整体代人; (4) 整体求和.
例如: $a b=1$. 求证: $\frac{1}{1+a}+\frac{1}{1+b}=1$.
证明: 左边 $=\frac{1}{1+a}+\frac{1}{1+b}=\frac{a b}{a b+a}+\frac{1}{1+b}=\frac{b}{1+b}+\frac{1}{1+b}=1=$ 右边.
波利亚在《怎样解题》中指出:“当你找到第一个藤㑬或作出第一个发现后, 再四处看看, 他们总是成群生长. ”针对类似问题,我们有更多的式子满足以上特征.
阅读材料二: 基本不等式 $\frac{a+b}{2} \geqslant \sqrt{a b}(a>0, b>0)$, 当且仅当 $a=b$ 时, 等号成立, 它是解决最值 问题的有力工具.
例如: 在 $x>0$ 的条件下, 当 $x$ 为何值时, $x+\frac{1}{x}$ 有最小值, 最小值是多少?
解: $\because x>0, \frac{1}{x}>0, \therefore \frac{x+\frac{1}{x}}{2} \geqslant \sqrt{x \cdot \frac{1}{x}}=1$, 即 $x+\frac{1}{x} \geqslant 2$.
当且仅当 $x=\frac{1}{x}$, 即 $x=1$ 时, $x+\frac{1}{x}$ 有最小值, 最小值为 2 .
请根据上述阅读材料,解答下列问题:
任务一:
(1)已知 $a b=1$, 则 $\frac{1}{1+a^2}+\frac{1}{1+b^2}=$
(2)已知 $a b=1$, 则 $\frac{1}{1+a^3}+\frac{1}{1+b^3}=$
任务二: 已知 $a b=1$, 证明 $\frac{1}{a^n+1}+\frac{1}{b^n+1}=1$.
任务三: 已知 $a b c=1$, 求 $\frac{3 a}{a b+a+1}+\frac{3 b}{b c+b+1}+\frac{3 c}{a c+c+1}$ 的值.
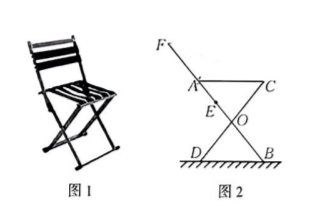
图 1 是简易座椅, 图 2 是其侧面示意图, 固定点 $O$ 为椅还 $A B$ 和 $C D$ 的中点, 靠背 $E F$ 的一端固 定在 $A O$ 上的 $E$ 点处, 将 $E F$ 绕点 $E$ 顺时针旋转 $180^{\circ}$ 后与 $E B$ 重合, 此时靠背收拢. 已知 $A B=$ $C D=40 \mathrm{~cm} . A E=10 \mathrm{~cm}, \angle A O C=74^{\circ}$.
(1)求坐垫 $A C$ 的长.
(2) 在收拢靠背的过程中.求点 $F$ 与点 $C$ 间距离的最小值.
(结果精确到 $1 \mathrm{~cm}$; 参考数据: $\sin 37^{\circ}=\cos 53^{\circ} \approx 0.6, \sin 53^{\circ}=\cos 37^{\circ} \approx 0.8, \tan 37^{\circ} \approx 0.75$, $\left.\tan 53^{\circ} \approx 1.33, \sqrt{97} \approx 9.85\right)$
问题情境:
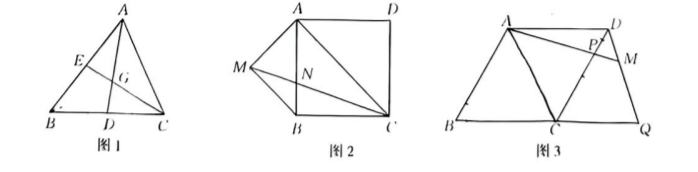
数学活动课上, 老师出示了一个问题: 如图 1, 在 $\triangle A B C$ 中, $D, E$ 分别是边 $B C, A B$ 的中点, $A D$, $C E$ 相交于点 $G$.
独立思考:
(1)试猜想 $G E$ 与 $C E$ 的数量关系, 并加以证明.
实践探究:
(2) 如图 2, 在正方形 $A B C D$ 中, $A B=4$, 以 $A B$ 为斜边作等腰直角 $\triangle A B M$, 使 $\angle A M B=90^{\circ}$, 连 接 $C M$ 交 $A B$ 于点 $N$,求 $\frac{B N}{C M}$ 的值.
问题解决:
(3) 如图 3, 在菱形 $A B C D$ 中, $\angle B=60^{\circ}$, 点 $P$ 在 $C D$ 边上, 点 $Q$ 在 $B C$ 的延长线上, 连接 $D Q, C P$ $=C Q$, 射线 $A P$ 交 $D Q$ 于点 $M$. 若 $A B=6, A P=\sqrt{31}$, 请直接写出 $D M$ 的长.
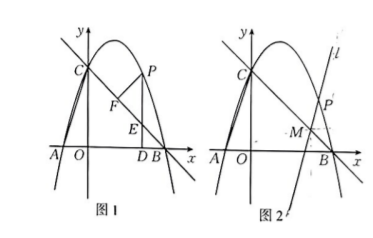
如图 1. 在平面直角坐标系 $x O y$ 中, 直线 $y=-x+3$ 分别交 $x$ 轴, $y$ 轴于点 $B, C$, 二次函数 $y=$ $a x^2+b x+c$ 的图象经过点 $B, C$, 且与 $x$ 轮的另一个交点为 $A$ ( $A$ 点在原点左侧), 若 $O B=3 O A$, $P$ 是第一象限内二次函数图象上的一个动点, 过点 $P$ 作 $P D \perp x$ 制于点 $D$, 交 $B C$ 于点 $E$, 作 $P F$ $\perp B C$ 于点 $F$.
(1) 求点 $A$ 的坐标及二次函数的表达式.
(2)当 $\triangle P E F$ 的周长最大时, 求点 $P$ 的坐标.
(3) 如图 2, 过点 $P$ 作 $A C$ 的平行线 $l$, 交线段 $B C$ 于点 $M$, 在直线 $l$ 上是否存在点 $N$, 使得以点 $A . C . M . N$ 为顶点的四边形为菱形? 若存在, 直接写出点 $N$ 的坐标; 若不存在, 请说明 理由.