问题情境:
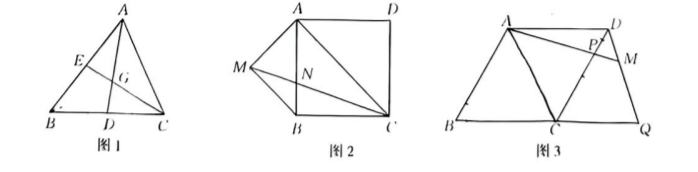
数学活动课上, 老师出示了一个问题: 如图 1, 在 $\triangle A B C$ 中, $D, E$ 分别是边 $B C, A B$ 的中点, $A D$, $C E$ 相交于点 $G$.
独立思考:
(1)试猜想 $G E$ 与 $C E$ 的数量关系, 并加以证明.
实践探究:
(2) 如图 2, 在正方形 $A B C D$ 中, $A B=4$, 以 $A B$ 为斜边作等腰直角 $\triangle A B M$, 使 $\angle A M B=90^{\circ}$, 连 接 $C M$ 交 $A B$ 于点 $N$,求 $\frac{B N}{C M}$ 的值.
问题解决:
(3) 如图 3, 在菱形 $A B C D$ 中, $\angle B=60^{\circ}$, 点 $P$ 在 $C D$ 边上, 点 $Q$ 在 $B C$ 的延长线上, 连接 $D Q, C P$ $=C Q$, 射线 $A P$ 交 $D Q$ 于点 $M$. 若 $A B=6, A P=\sqrt{31}$, 请直接写出 $D M$ 的长.