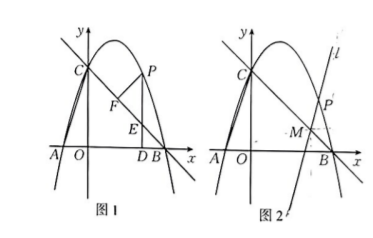
如图 1. 在平面直角坐标系 $x O y$ 中, 直线 $y=-x+3$ 分别交 $x$ 轴, $y$ 轴于点 $B, C$, 二次函数 $y=$ $a x^2+b x+c$ 的图象经过点 $B, C$, 且与 $x$ 轮的另一个交点为 $A$ ( $A$ 点在原点左侧), 若 $O B=3 O A$, $P$ 是第一象限内二次函数图象上的一个动点, 过点 $P$ 作 $P D \perp x$ 制于点 $D$, 交 $B C$ 于点 $E$, 作 $P F$ $\perp B C$ 于点 $F$.
(1) 求点 $A$ 的坐标及二次函数的表达式.
(2)当 $\triangle P E F$ 的周长最大时, 求点 $P$ 的坐标.
(3) 如图 2, 过点 $P$ 作 $A C$ 的平行线 $l$, 交线段 $B C$ 于点 $M$, 在直线 $l$ 上是否存在点 $N$, 使得以点 $A . C . M . N$ 为顶点的四边形为菱形? 若存在, 直接写出点 $N$ 的坐标; 若不存在, 请说明 理由.
(1) 求点 $A$ 的坐标及二次函数的表达式.
(2)当 $\triangle P E F$ 的周长最大时, 求点 $P$ 的坐标.
(3) 如图 2, 过点 $P$ 作 $A C$ 的平行线 $l$, 交线段 $B C$ 于点 $M$, 在直线 $l$ 上是否存在点 $N$, 使得以点 $A . C . M . N$ 为顶点的四边形为菱形? 若存在, 直接写出点 $N$ 的坐标; 若不存在, 请说明 理由.
