单选题 (共 8 题 ),每题只有一个选项正确
计算 $(-\sqrt{11})^2$ 的结果为
$\text{A.}$ $-11$
$\text{B.}$ $11$
$\text{C.}$ $\pm 11$
$\text{D.}$ $121$
下列二次根式与 $\sqrt{3}$ 是同类二次根式的是
$\text{A.}$ $\sqrt{12}$
$\text{B.}$ $\sqrt{18}$
$\text{C.}$ $\sqrt{30}$
$\text{D.}$ $\sqrt{\frac{2}{3}}$
一元二次方程 $x^2+x-2=0$ 根的判别式的值为
$\text{A.}$ $-7$
$\text{B.}$ $3$
$\text{C.}$ $9$
$\text{D.}$ $\pm 3$
若将抛物线 $y=x^2-1$ 向上平移 3 个单位后所得的抛物线记为 $G$, 则抛物线 $G$ 对应的 $y$ 与 $x$ 之 间的函数关系式为
$\text{A.}$ $y=(x-3)^2-1$.
$\text{B.}$ $y=(x+3)^2-1$.
$\text{C.}$ $y=x^2-4$.
$\text{D.}$ $y=x^2+2$.
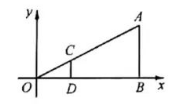
如图, 在平面直角坐标系中, 有点 $A(6,3), B(6,0)$, 以原点 $O$ 为位似中心, 在第一象 限内将线段 $A B$ 缩小后得到线段 $C D$, 点 $A$ 的对应点为点 $C$. 若 $\triangle O C D$ 与 $\triangle O A B$ 的相似比为 $\frac{1}{3}$, 则点 $C$ 的坐标为
$\text{A.}$ $(2,1)$.
$\text{B.}$ $(2,0)$.
$\text{C.}$ $(3,1)$.
$\text{D.}$ $(3,0)$.
如图, $O$ 为跷跷板 $A B$ 的中点. 支柱 $O C$ 与地面 $D E$ 垂直, 垂足为点 $C$, 当跷跷板的一端 $B$ 着地时, 跷跷板 $A B$ 与地面 $D E$ 的夹角为 $26^{\circ}$, 经测得 $A B=1.8 \mathrm{~m}$, 则 $O C$ 的长为

$\text{A.}$ $0.9 \cos 26^{\circ} \mathrm{m}$.
$\text{B.}$ $0.9 \sin 26^{\circ} \mathrm{m}$.
$\text{C.}$ $\frac{0.9}{\sin 26^{\circ}} \mathrm{m}$.
$\text{D.}$ $\frac{0.9}{\cos 26^{\circ}} \mathrm{m}$.
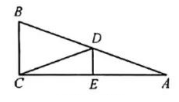
如图, 在 $\triangle A B C$ 中, $\angle A C B=90^{\circ}, C D$ 是斜边 $A B$ 的中线, 过点 $D$ 作 $D E \perp A C$, 垂足为点 $E$. 若 $\sin A=\frac{1}{3}, A B=6$, 则 $\triangle C D E$ 的周长为
$\text{A.}$ $4+2 \sqrt{2}$.
$\text{B.}$ $4+4 \sqrt{2}$.
$\text{C.}$ $6+2 \sqrt{2}$.
$\text{D.}$ $6+4 \sqrt{2}$.
抛物线 $y=a x^2+b x+c(a < 0)$ 的对称轴为直线 $x=2$, 与 $x$ 轴的一个交点坐标为 $(5,0)$, 其部 分图象如图所示, 则下列结论错误的是

$\text{A.}$ $a b c < 0$.
$\text{B.}$ 方程 $a x^2+b x+c=0$ 的两个根是 $x_1=-1, x_2=5$.
$\text{C.}$ $b+4 a=0$.
$\text{D.}$ 若 $y > 0$, 则 $x$ 的取值范围是 $0 < x < 5$.
填空题 (共 6 题 ),请把答案直接填写在答题纸上
计算: $\sqrt{28} \div \sqrt{7}=$.
某校篮球队进行篮球训练, 某队员投篮的统计结果如下表, 根据表中数据可知该队员一次 投篮命中的概率大约是

如图, $A D 、 B C$ 相交于点 $O$, 点 $E 、 F$ 分别在 $B C 、 A D$ 上, $A B / / C D / / E F$. 若 $C E=6, E O=4$, $B O=5, A F=6$, 则 $A D=$

如图①, 西周数学家商高用 “矩” 测量物高的方法: 把矩的两边放置成如图②的位置, 从 矩的一端 $A$ (人眼) 望点 $E$, 使视线通过点 $C$, 记人站立的位置为点 $B$, 量出 $B G$ 的长, 即 可算得物高 $E G$. 经测量, 得 $a=60 \mathrm{~cm}, b=120 \mathrm{~cm}, A B=1.5 \mathrm{~m}$. 设 $B G=x(\mathrm{~m}), E G=y(\mathrm{~m})$, 则 $y$ 与 $x$ 之间的函数关系式为

如图, 在 $\triangle A B C$ 中, $\angle C=90^{\circ}$, 作 $\angle C A D=\angle B$ 交边 $B C$ 于点 $D$. 若 $\tan B=\frac{2}{3}$, 则 $\cos \angle A D C$ 的值为

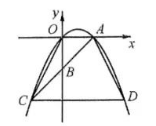
如图, 在平面直角坐标系中, $O$ 为坐标原点, 抛物线 $y=-\frac{1}{2} x^2+b x$ 与 $x$ 轴正半轴交于点 $A$, 点 $B$ 是 $y$ 轴负半轴上一点, 点 $A$ 关于点 $B$ 的对称点 $C$ 在该抛物线上, 过点 $C$ 作 $y$ 轴的垂线 交抛物线于点 $D$, 连结 $O C 、 A D$. 若点 $C$ 的横坐标为 -2 , 则四边形 $O C D A$ 的面积为
解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $\sqrt{2} \cdot \cos 45^{\circ}-\sin ^2 60^{\circ}+\tan 45^{\circ}$.
在一个不透明的盒子中装有三张卡片, 分别标有数字为 $1 、 2 、 3$, 这些卡片除数字不同外 其余均相同. 洗匀后, 小吉从盒子中随机抽取一张卡片记下数字后放回, 洗匀后再随机抽取一张 卡片. 用画树状图或列表的方法, 求两次抽取的卡片上数字之和为奇数的概率.
2022 年北京冬奥会的吉祥物 “冰墩撴” 深受国内外广大朋友的喜爱, 北京奥组委会 官方也推出了许多吉祥物的周边产品. 某特许零售店发现该 “冰墩墩” 的销售非常火爆. 据统计, 该店 2021 年 10 月的销量为 1 万件, 2021 年 12 月的销量为 1.21 万件. 若该店 “冰墩墩” 销量的月平均增长率保持不变, 求该店 “冰墩墩” 销量的月平均增长率.
如图, 在平面直角坐标系中, $O$ 为坐标原点, 抛物线 $y=x^2-3 x$ 与 $x$ 轴的另一交点为 点 $A$,与 $y$ 轴垂直的直线 $l$ 交该抛物线于点 $B$ 和点 $C$, 设点 $B$ 的纵坐标为 $n$
(1) 求线段 $O A$ 的长.
(2) 当函数值 $y$ 随 $x$ 增大而增大时, 直接写出自变量 $x$ 的取值范围.
(3) 当线段 $B C$ 的长小于 $O A$ 时, 直接写出 $n$ 的取值范围.

图①、图②、图③都是 $6 \times 6$ 的网格, 每个小正方形的顶点称为格点, 每个小正方形 的边长均为 1. $\triangle A B C$ 顶点均在格点上. 在图①、图②、图③给定的网格中, 仅用无刻度的 直尺, 按下列要求完成画图, 并保留作图痕迹,
(1) 在图①中画 $\triangle A B C$ 的高 $C D$.
(2) 在图②中画 $\triangle A B C$ 的中位线 $E F$, 使点 $E 、 F$ 分别在边 $A B 、 A C$ 上.
(3) 在图③中画 $\triangle A G H$, 使 $\triangle A B M \sim \triangle A G H, \triangle A B M$ 与 $\triangle A G H$ 的相似比为 $\frac{2}{3}$, 且 $A H \perp B C$ 于点 $M$.

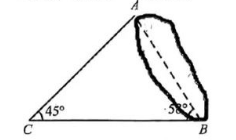
如图, 一个水池的两端分别为 $A 、 B$ 两点, 在岸上选一点 $C$, 使点 $C$ 能直接到达 $A$ 、 $B$ 两点, 连结 $A C 、 B C$. 经测得 $B C=221 \mathrm{~m}, \angle A B C=58^{\circ}, \angle A C B=45^{\circ}$, 求 $A, B$ 两点之 间的距离 (结果保留整数). (参考数据: $\sin 58^{\circ} \approx 0.85, \cos 58^{\circ} \approx 0.53, \tan 58^{\circ} \approx 1.60$.)
如图①, 有一个直径为 $20 \mathrm{~m}$ 的圆形喷水池, 四周安装一圈喷头, 喷射水柱呈抛物线型, 在水池中心 $O$ 处立着一个直径为 $0.8 \mathrm{~m}$ 的圆柱形实心石柱, 各方向喷出的水柱在石柱顶部的中心点 $M$ 处汇合. 如图②, 水柱距水池中心 $4 \mathrm{~m}$ 处到达最大高度为 $6 \mathrm{~m}$, 建立如图② 所示的平面直角坐标系.
(1) 选择图②中一条抛物线求其对应的函数关系式.
(2) 求点 $M$ 的纵坐标.
(3). 如图③, 在水池里过水池中心的直线上安装一排直线型喷头, 且喷射水柱竖直向上, 高度均为 $\frac{21}{8} \mathrm{~m}$, 相邻两个直线型喷头的间距均为 $1.2 \mathrm{~m}$, 且喷射的水柱不能碰到拋物线 型水柱, 要求在符合条件处都安装喷头, 安装后关于 $O M$ 成轴对称分布, 且每相邻的 两个直线型喷头的间距为 $1.2 \mathrm{~m}$. 直接写出离中心 $O$ 最远的两个直线型喷头的水平距离.

【操作一】 如图①, 将矩形 $A B C D(A B>A D)$ 沿过点 $D$ 的直线折叠, 使点 $A$ 的对称 点 $F$ 落在边 $C D$ 上, 折痕为 $D E$. 则 $\angle D E F$ 的大小为 度.
【操作二】如图①, 在操作一的基础上, 将矩形 $A B C D$ 沿过点 $C$ 的直线折叠, 点 $B$ 的对称 点 $H$ 落在边 $E F$ 上, 折痕为 $C G$. 求证: $\triangle C F H \backsim \triangle H E G$.
【应用】如图②, 延长图①中的 $G H$ 交边 $D E$ 于点 $M$. 若 $A B=16, A D=10$, 则 $E H$ 的长 为 , 点 $M$ 到边 $E F$ 的距离为
【拓展】 如图③, 点 $N$ 为【操作二】图(1)中的边 $D E$ 上的点, 连结 $H N 、 C N$. 若 $A B=16$, $A D=10$, 则 $H N+C N$ 的最小值为

如图, 在 Rt $\triangle A B C$ 中, $\angle C=90^{\circ}, A B=8, A C=6, D$ 是边 $A B$ 的中点. 动点 $P$ 从点 $A$ 出发, 以每秒 4 个单位长度的速度沿 $A B$ 向终点 $B$ 运动, 过点 $P$ 作 $P Q \perp A C$ 于点 $Q$, 当点 $P$ 不与点 $A 、 D 、 B$ ) 重合时, 以 $P D 、 P Q$ 为邻边作 $\square P D E Q$, 设点 $P$ 的运动时间为 $t$ 秒.
(1) 用含有 $t$ 的代数式表示线段 $D E$ 的长.
(2) 当点 $E$ 到点 $A 、 D$ 的距离相等时, 求 $D E$ 的长.
(3) 当 $\square P D E Q$ 的某条对角线与边 $A B$ 垂直时, 求 $t$ 的值.
(4) 作点 $P$ 关于直线 $D E$ 的对称点 $P^{\prime}$, 连结 $P^{\prime} Q$, 当 $\angle P Q P^{\prime}=\angle A$ 时, 直接写出 $t$ 的值.

在平面直角坐标系中, $O$ 为坐标原点, 点 $A(-1,0) 、 B\left(0,-\frac{5}{2}\right)$ 在抛物线 $y=\frac{1}{2} x^2+b x+c$ 上, 点 $C$ 为该抛物线的顶点. 点 $P$ 为该抛物线上一点, 其横坐标为 $m$.
(1) 求该抛物线对应的函数关系式.
(2) 连结 $B P$, 当 $B P \perp y$ 轴时, 顺次连结点 $A 、 B 、 C 、 P$, 求四边形 $A B C P$ 的面积.
(3) 当 $m>0$ 时, 设该抛物线在点 $B$ 与点 $P$ 之间 (包含点 $B$ 和点 $P$ ) 的部分图象的最低点和 最高点到 $x$ 轴的距离分别为 $k 、 n$, 若 $k-n=2$, 求 $m$ 的取值范围.
(4) 当点 $P$ 在第四象限时, 作点 $P$ 关于点 $O$ 的对称点 $Q$, 以 $P Q$ 为对角线构造矩形 $P M Q N$, 该矩形的边均与坐标轴垂直, 且点 $A 、 B$ 在该矩形的内部. 设抛物线在该矩形内部及边 界的图象记为 $G$, 图象 $G$ 的最高点与最低点的纵坐标之差为 $d$, 最低点在该矩形边所在 的直线记为 $l$, 若点 $C$ 到直线 $l$ 的距离等于 $\frac{1}{7} d$, 直接写出 $m$ 的值.