阅读与思考
下面是小宇同学的数学小论文,请仔细阅读并完成相应的任务
用函数观点认识一元二次方程根的情况
我们知道, 一元二次方程 $a x^2+b x+c=0(a \neq 0)$ 的根就是相应的二次函数 $y=a x^2+b x+c(a \neq 0)$ 的图象 (称为拋物线) 与 $x$ 轴交点的横坐标. 抛物线与 $x$ 轴的交点有三种情况: 有两个交点、有一个交点、无交点. 与此相对应, 一元二次方程的根也有三种情况:有两个不相等的实数根、有两个相等的实数根、无实数根. 因此可用抛物线与 $x$ 轴的交点个数确定一元二次方程根的情况.
下面根据拋物线的顶点坐标 $\left(-\frac{b}{2 a}, \frac{4 a c-b^2}{4 a}\right)$ 和一元二次方程根的判别式 $\Delta=b^2-4 a c$, 分别从 $a>0$ 和 $a < 0$ 两种情况进行分析:
(1) $a>0$ 时, 拋物线开口向上.
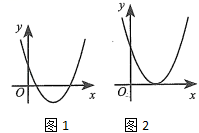
①当 $\Delta=b^2-4 a c>0$ 时, 有 $4 a c-b^2 < 0 . \because a>0, \therefore$ 顶点纵坐标 $\frac{4 a c-b^2}{4 a} < 0$.
$\therefore$ 顶点在 $x$ 轴的下方, 抛物线与 $x$ 轴有两个交点 (如图 1).
②当 $\Delta=b^2-4 a c=0$ 时, 有 $4 a c-b^2=0 . \because a>0, \therefore$ 顶点纵坐标 $\frac{4 a c-b^2}{4 a}=0$.
$\therefore$ 顶点在 $x$ 轴上, 拋物线与 $x$ 轴有一个交点 (如图 2).
$\therefore$ 一元二次方程 $a x^2+b x+c=0 \quad(a \neq 0)$ 有两个相等的实数根.
③当 $\Delta=b^2-4 a c < 0$ 时,
(2) $a < 0$ 时, 抛物线开口向下.
任务: (1) 上面小论文中的分析过程, 主要运用的数学思想是 (从下面选项中选 出两个即可);
A. 数形结合
B. 统计思想
C. 分类讨论
D. 转化思想
(2) 请参照小论文中当 $a>0$ 时(1)(2)的分析过程, 写出(3)中当 $a>0, \Delta < 0$ 时, 一元二次方程根的情况的分析过程, 并画出相应的示意图;
(3) 实际上, 除一元二次方程外, 初中数学还有一些知识也可以用函数观点来认识, 例如: 可用函数观点来认识一元一次方程的解请你再举出一例为