综合与实践
问题情境: 在 Rt $\triangle \mathrm{ABC}$ 中, $\angle \mathrm{BAC}=90^{\circ}, \mathrm{AB}=6, \mathrm{AC}=8$. 直角三角板 $\mathrm{EDF}$ 中 $\angle \mathrm{EDF}=90^{\circ}$, 将三角板的直角顶点 $\mathrm{D}$ 放在 Rt $\triangle \mathrm{ABC}$ 斜边 $\mathrm{BC}$ 的中点处, 并将三角板绕点 $\mathrm{D}$ 旋转, 三 角板的两边 $\mathrm{DE}, \mathrm{DF}$ 分别与边 $\mathrm{AB}, \mathrm{AC}$ 交于点 $\mathrm{M}, \mathrm{N}$, 猜想证明:
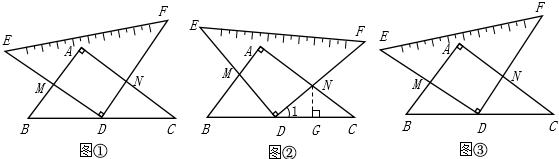
(1) 如图①, 在三角板旋转过程中, 当点 $\mathrm{M}$ 为边 $\mathrm{AB}$ 的中点时, 试判断四边形 $\mathrm{AMDN}$ 的 形状, 并说明理由; 问题解决:
(2) 如图②, 在三角板旋转过程中, 当 $\angle \mathrm{B}=\angle \mathrm{MDB}$ 时, 求线段 $\mathrm{CN}$ 的长;
(3) 如图③, 在三角板旋转过程中, 当 $\mathrm{AM}=\mathrm{AN}$ 时, 直接写出线段 $\mathrm{AN}$ 的长.
问题情境: 在 Rt $\triangle \mathrm{ABC}$ 中, $\angle \mathrm{BAC}=90^{\circ}, \mathrm{AB}=6, \mathrm{AC}=8$. 直角三角板 $\mathrm{EDF}$ 中 $\angle \mathrm{EDF}=90^{\circ}$, 将三角板的直角顶点 $\mathrm{D}$ 放在 Rt $\triangle \mathrm{ABC}$ 斜边 $\mathrm{BC}$ 的中点处, 并将三角板绕点 $\mathrm{D}$ 旋转, 三 角板的两边 $\mathrm{DE}, \mathrm{DF}$ 分别与边 $\mathrm{AB}, \mathrm{AC}$ 交于点 $\mathrm{M}, \mathrm{N}$, 猜想证明:
(1) 如图①, 在三角板旋转过程中, 当点 $\mathrm{M}$ 为边 $\mathrm{AB}$ 的中点时, 试判断四边形 $\mathrm{AMDN}$ 的 形状, 并说明理由; 问题解决:
(2) 如图②, 在三角板旋转过程中, 当 $\angle \mathrm{B}=\angle \mathrm{MDB}$ 时, 求线段 $\mathrm{CN}$ 的长;
(3) 如图③, 在三角板旋转过程中, 当 $\mathrm{AM}=\mathrm{AN}$ 时, 直接写出线段 $\mathrm{AN}$ 的长.
