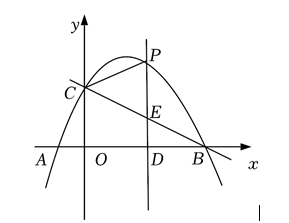
如图, 二次函数 $y=-\frac{1}{4} x^2+\frac{3}{2} x+4$ 的图象与 $\mathrm{x}$ 轴交于 $\mathrm{A}, \mathrm{B}$ 两点 (点 $\mathrm{A}$ 在点 $\mathrm{B}$ 的左侧), 与 $\mathrm{y}$ 轴交于点 $\mathrm{C}$, 点 $\mathrm{P}$ 是第一象限内二次函数图象上的一个动点, 设点 $\mathrm{P}$ 的横坐标为 $\mathrm{m}$. 过 点 $P$ 作直线 $P D \perp x$ 轴于点 $D$, 作直线 $B C$ 交 $P D$ 于点 $E$
(1) 求 $\mathrm{A}, \mathrm{B}, \mathrm{C}$ 三点的坐标, 并直接写出直线 $\mathrm{BC}$ 的函数表达式;
(2) 当 $\triangle C E P$ 是以 $P E$ 为底边的等腰三角形时, 求点 $P$ 的坐标;
(3) 连接 $\mathrm{AC}$, 过点 $\mathrm{P}$ 作直线 $l / / \mathrm{AC}$, 交 $\mathrm{y}$ 轴于点 $\mathrm{F}$, 连接 DF.试探究: 在点 $\mathrm{P}$ 运动的过 程中, 是否存在点 $\mathrm{P}$, 使得 $\mathrm{CE}=\mathrm{FD}$, 若存在, 请直接写出 $\mathrm{m}$ 的值; 若不存在, 请说明理 由.
(1) 求 $\mathrm{A}, \mathrm{B}, \mathrm{C}$ 三点的坐标, 并直接写出直线 $\mathrm{BC}$ 的函数表达式;
(2) 当 $\triangle C E P$ 是以 $P E$ 为底边的等腰三角形时, 求点 $P$ 的坐标;
(3) 连接 $\mathrm{AC}$, 过点 $\mathrm{P}$ 作直线 $l / / \mathrm{AC}$, 交 $\mathrm{y}$ 轴于点 $\mathrm{F}$, 连接 DF.试探究: 在点 $\mathrm{P}$ 运动的过 程中, 是否存在点 $\mathrm{P}$, 使得 $\mathrm{CE}=\mathrm{FD}$, 若存在, 请直接写出 $\mathrm{m}$ 的值; 若不存在, 请说明理 由.
