单选题 (共 2 题 ),每题只有一个选项正确
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的离心率为 $\sqrt{5}, C$ 的一条渐近线与圆 $(x-2)^2+(y-3)^2=1$ 交于 $A, B$两点,则 $|A B|=(\quad)$
$\text{A.}$ $\frac{\sqrt{5}}{5}$
$\text{B.}$ $\frac{2 \sqrt{5}}{5}$
$\text{C.}$ $\frac{3 \sqrt{5}}{5}$
$\text{D.}$ $\frac{4 \sqrt{5}}{5}$
设 $F$ 为抛物线 $C: y^2=4 x$ 的焦点,点 $A$ 在 $C$ 上,点 $B(3,0)$ ,若 $|A F|=|B F|$ ,则 $|A B|=(\quad)$
$\text{A.}$ 2
$\text{B.}$ $2 \sqrt{2}$
$\text{C.}$ 3
$\text{D.}$ $3 \sqrt{2}$
多选题 (共 3 题 ),每题有多个选项正确
设 $O$ 为坐标原点,直线 $y=-\sqrt{3}(x-1)$ 过抛物线 $C: y^2=2 p x(p>0)$ 的焦点,且与 $C$ 交于 $M, N$ 两点,$l$ 为 $C$的准线,则( )
$\text{A.}$ $p=2$
$\text{B.}$ $|M N|=\frac{8}{3}$
$\text{C.}$ 以 $M N$ 为直径的圆与 $l$ 相切
$\text{D.}$ $\triangle O M N$ 为等腰三角形
已知 $O$ 为坐标原点,点 $A(1,1)$ 在抛物线 $C: x^2=2 p y(p>0)$ 上,过点 $B(0,-1)$ 的直线交 $C$ 于 $P, Q$ 两点,则
$\text{A.}$ $C$ 的准线为 $y=-1$
$\text{B.}$ 直线 $A B$ 与 $C$ 相切
$\text{C.}$ $|O P| \cdot|O Q|>|O A|^2$
$\text{D.}$ $|B P| \cdot|B Q|>|B A|^2$
已知 $O$ 为坐标原点,过抛物线 $C: y^2=2 p x(p>0)$ 焦点 $F$ 的直线与 $C$ 交于 $A$ , $B$ 两点,其中 $A$ 在第一象限,点 $M(p, 0)$ .若 $|A F|=|A M|$ ,则( )
$\text{A.}$ 直线 $A B$ 的斜率为 $2 \sqrt{6}$
$\text{B.}$ $|O B|=|O F|$
$\text{C.}$ $|A B|>4|O F|$
$\text{D.}$ $\angle O A M+\angle O B M < 180^{\circ}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
已知直线 $l$ 与椭圆 $\frac{x^2}{6}+\frac{y^2}{3}=1$ 在第一象限交于 $A, B$ 两点,$l$ 与 $x$ 轴、 $y$ 轴分别相交于 $M, N$ 两点,且 $|M A|=|N B|,|M N|=2 \sqrt{3}$ ,则 $l$ 的方程为
记双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的离心率为 $e$ ,写出满足条件"直线 $y=2 x$ 与 $C$ 无公共点"的 $e$ 的一个值 $\qquad$ .
以 $A(2,1)$ 为中点的双曲线 $C: 2 x^2-y^2=2$ 的弦所在直线的方程为
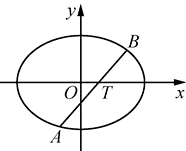
如图,已知椭圆 $C: \frac{x^2}{8}+\frac{y^2}{4}=1$ .过点 $T(1,0)$ 作斜率为 $k(k>0)$ 的直线 $l$ 交椭圆 $C$ 于 $A, B$ 两点(点 $A$ 在 $x$ 轴的下方).若 $\overrightarrow{A T}=2 \overrightarrow{T B}$ ,求直线 $l$ 的斜率 $k$ .
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的右焦点为 $F(2,0)$ ,渐近线方程为 $y= \pm \sqrt{3} x$ .
(1)求 $C$ 的方程;
(2)过 $F$ 的直线与 $C$ 的两条渐近线分别交于 $A, B$ 两点,点 $P\left(x_1, y_1\right), Q\left(x_2, y_2\right)$ 在 $C$ 上,且 $x_1>x_2>0$ , $y_1>0$ .过 $P$ 且斜率为 $-\sqrt{3}$ 的直线与过 $Q$ 且斜率为 $\sqrt{3}$ 的直线交于点 $M$ .从下面(1)(2)(3)中选取两个作为条件,证明另外一个成立.
(1)$M$ 在 $A B$ 上;
(2)$P Q / / A B$ ;
(3)$|M A|=|M B|$ .
注:若选择不同的组合分别解答,则按第一个解答计分.
已知直线 1: $\mathrm{y}=\mathrm{kx}+2$ ,椭圆 $\mathrm{C}: \frac{\mathrm{x}^2}{4}+\mathrm{y}^2=1$ .试问当 k 取何值时,直线 1 与椭圆 C :
(1)有两个不重合的公共点;
(2)有且只有一个公共点;
(3)没有公共点.
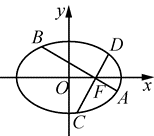
如图,在平面直角坐标系 $x O y$ 中,椭圆 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的离心率为 $\frac{1}{2}$ ,过椭圆右焦点 $F$ 作两条互相垂直的弦 $A B$ 与 $C D$ .当直线 $A B$ 的斜率为 0 时,$A B=4$ .
(1)求椭圆的方程;
(2)若 $A B+C D=\frac{48}{7}$ ,求直线 $A B$ 的方程.
已知抛物线 $C: y^2=3 x$ 的焦点为 $F$ ,斜率为 $\frac{3}{2}$ 的直线 $l$ 与抛物线 $C$ 的交点为 $A, B$ ,与 $x$ 轴的交点为 $P$ .
(1)若 $A F+B F=4$ ,求直线 $l$ 的方程;
(2)若 $\overrightarrow{A P}=3 \overrightarrow{P B}$ ,求 $A B$ 的长.