单选题 (共 12 题 ),每题只有一个选项正确
赤道长约为 $40000000 \mathrm{~m}$, 用科学记数法可以把数字 $40000000$ 表示为
$\text{A.}$ $4 \times 10^7 $
$\text{B.}$ $ 40 \times 10^6$
$\text{C.}$ $400 \times 10^5$
$\text{D.}$ $4000 \times 10^3$
中国是最早采用正负数表示相反意义的量, 并进行负数运算的国家。若零上 $10^{\circ} \mathrm{C}$ 记作$+10^{\circ} \mathrm{C}$, 则零下 $10^{\circ} \mathrm{C}$ 可记作
$\text{A.}$ $10^{\circ} \mathrm{C}$
$\text{B.}$ $0^{\circ} \mathrm{C}$
$\text{C.}$ $-10{ }^{\circ} \mathrm{C}$
$\text{D.}$ $-20^{\circ} \mathrm{C}$
如图, 已知直线 $c$ 与直线 $a 、 b$ 都相交. 若 $a / / b, \angle 1=85^{\circ}$, 则 $\angle 2=$
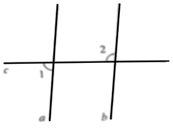
$\text{A.}$ $110^{\circ}$
$\text{B.}$ $105^{\circ}$
$\text{C.}$ $100^{\circ}$
$\text{D.}$ $95^{\circ}$
反比例函数 $\mathrm{y}=\frac{6}{x}$ 的图象分别位于
$\text{A.}$ 第一、第三象限
$\text{B.}$ 第一、第四象限
$\text{C.}$ 第二、第三象限
$\text{D.}$ 第二、第四象限
如图, 在 $\triangle A B C$ 中, $D 、 E$ 分别为线段 $B C 、 B A$ 的中点, 设 $\triangle A B C$ 的面积为 $S_1$, $\Delta \mathrm{EBD}$
的面积为 $S_2$. 则 $\frac{s_1}{s_2}=$
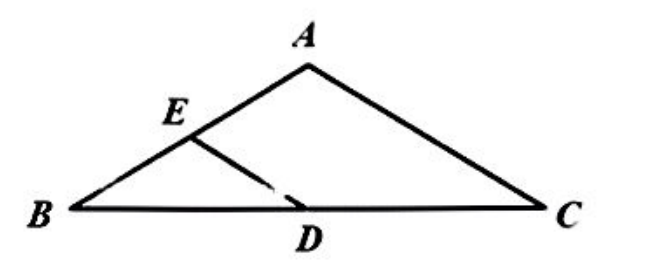
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{3}{4}$
$\text{D.}$ $\frac{7}{8}$
为庆祝中国共产主义青年团建团100周年,某校团委组织以“扬爱国精神,展青春风采”为主题的合唱活动,下表是九年级一班的得分情况

数据 $9.9,9.7,9.6,10,9.8$ 的中位数是
$\text{A.}$ 9.6
$\text{B.}$ 9.7
$\text{C.}$ 9.8
$\text{D.}$ 9.9
下列图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图),则这个几何体是
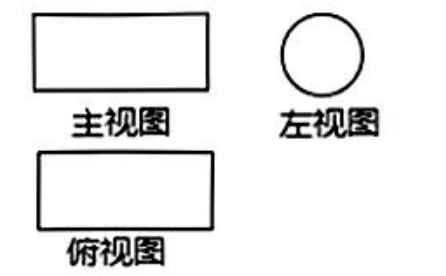
$\text{A.}$ 三棱柱
$\text{B.}$ 三棱锥
$\text{C.}$ 圆柱
$\text{D.}$ 圆锥
按一定规律排列的单项式 : $x, 3 x^2, 5 x^3, 7 x^4, 9 x^5, \ldots \ldots$, 第 $n$ 个单项式是
$\text{A.}$ $(2 \mathrm{n}-1) x^n$
$\text{B.}$ $(2 \mathrm{n}+1) x^n$
$\text{C.}$ $(\mathrm{n}-1) x^n$
$\text{D.}$ $(\mathrm{n}+1) x^n$
如图, 已知 $A B$ 是 $\odot O$ 的直径, $C D$ 是 $O O$ 的弦, $A B \perp C D$. 重足为 $E$. 著 $A B=26, C D=24$,则 $\angle \mathrm{OCE}$

$\text{A.}$ $\frac{7}{13}$
$\text{B.}$ $\frac{7}{12}$
$\text{C.}$ $\frac{12}{13}$
$\text{D.}$ $\frac{13}{12}$
下列运算正确的是
$\text{A.}$ $\sqrt{2}+\sqrt{3}=\sqrt{5}$
$\text{B.}$ $3^0=0$
$\text{C.}$ $(-2 a)^3=-8 a^3$
$\text{D.}$ $a^6 \div a^3=a^2$
如图, $O B$ 平分 $\angle A O C, D 、 E 、 F$ 分别是射线 $O A$ 、射线 $O B 、$ 射线 $O C$ 上的点, $D 、 E 、 F$ 与 $O$ 点都不重合, 连接 $E D 、 E F$ 若添加下列条件中的某一个.就能使 $\triangle D O E$ $\cong \triangle \mathrm{FOE}$, 你认为要添加的那个条件是
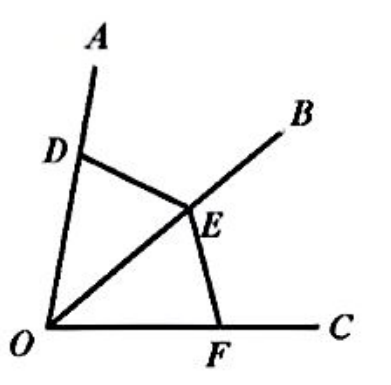
$\text{A.}$ $\mathrm{OD}=\mathrm{OE}$
$\text{B.}$ $\mathrm{OE}=\mathrm{OF}$
$\text{C.}$ $\angle \mathrm{ODE}=\angle \mathrm{OED}$
$\text{D.}$ $\angle \mathrm{ODE}=\angle \mathrm{OFE}$
某地开展建设绿色家园活动,活动期间,计划每天种植相同数量的树木,该活动开始
后、实际每天比原计划每天多植树50棵,实际植树 400棵所需时间与原计划植树300
棵所需时间相同。设实际每天植树x棵.则下列方程正确的是
$\text{A.}$ $\frac{400}{x-50}=\frac{300}{x}$
$\text{B.}$ $\frac{300}{x+50}=\frac{400}{x}$
$\text{C.}$ $\frac{400}{x+50}=\frac{300}{x}$
$\text{D.}$ $\frac{300}{x+50}=\frac{400}{x}$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
若 $\sqrt{x+1}$ 有意义, 则实数 $\mathrm{x}$ 的取值范围为
点 $A(1,-5)$ 关于原点的对称点为点 $B$, 则点 $B$ 的坐标为
某中学开展劳动实习, 学生到教具加工厂制作圆雉, 他们制作的圆锥, 母线长为 $30 \mathrm{~cm}$, 底面圆的半径为 $10 \mathrm{~cm}$; 这种锥的侧面展开图的圆心角度数是
已知 $\triangle A B C$ 是等腰三角形. 若 $\angle A=40^{\circ}$, 则 $\triangle A B C$ 的顶角度数是
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
临近端午节,某学校数学兴趣小组到社区参加社会实践活动,帮助有关部门了解某小区居民对去年销量较好的鲜花棕、火腿棕、豆沙粽、蛋黄粽四种粽子的喜爱情况.在对该小区 居民进行抽样调查后,根据统计结果绘制如下统计图∶
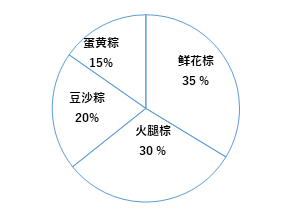

说明∶参与本次抽样调查的每一位居民在上述四种粽子中选择且只选择了一种喜爱的粽子. 谐根据以上信息,解答下列问题∶
(1)补全条形统计图∶
(2)若该小区有 1820人,估计喜爱火腿粽的有多少人?
某班甲、乙两名同学被推在到学校艺术节上表演节目,计划用葫芦丝合奏一首乐曲,要合奏的乐曲是用游戏的方式在《月光下的凤尾竹》与《彩云之南》中确定一首.
游戏规则如下;在一个不透明的口袋中装有分别标有数字1.2,3,4的四个小球(除标号外,其余都相同),甲从口袋中任意摸出1个小球,小球上的数字记为a.在另一个不透明的口袋中装有分别标有数字1,2的两张卡片(除标号外,其余都相同),乙从口袋里任意摸出1张卡片卡片上的数字记为b.然后计算这两个数的和,即a+b
若a+b为奇数,则演奏《月光下的凤尾竹》,否则,演奏(彩云之南》.
(1)用列表法或画树状图法中的一种方法,求(a,b)所有可能出现的结果总数;
(2)你认为这个游戏公平剪?如果公平,请说明理由;如果不公平,哪一首乐曲更可
能被选中?
如图; 在平行四边形 $A B C D$ 中, 连接 $B D, E$ 为线段 $A D$ 的中点, 延长 $B E$ 与 $C D$ 的延长线交于点 $\mathrm{F}$, 连接 $\mathrm{AF}, \angle \mathrm{BDF}=90^{\circ}$
(1) 求证:四边形 $A B D F$ 是矩形;
(2) 若 $A D=5, D F=3$, 求四边形 $A B C F$ 的面积 $S$.

某学校要购买甲、乙两种消毒液,用于预防新型冠状病霉.若购买9桶甲消毒液和6桶乙消毒液,则一共需要615元∶若购买8桶甲消毒液和12桶乙消毒液,则一共需要780元.
(1)每桶甲消毒液、每桶乙消毒液的价格分别是多少元?
(2)若该校计划购买甲、乙两种消毒液共 30 桶,其中购买甲消毒液a桶,且甲消毒液
的数量至少比乙消毒液的数量多5桶,又不超过乙消毒液的数量的2倍。怎样购买。才能使总费用W最少?并求出最少费用
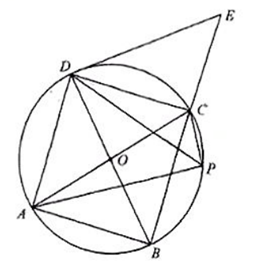
如图, 四边形 $A B C D$ 的外接圆是以 $B D$ 为直径的 $\odot O, P$ 是 $\odot O$ 的劣狐 $B C$ 上 的任 $E$ 意一点连接 $P A 、 P C 、 P D$, 延长 $B C$ 至 $E$, 使 $B D^2=B C \cdot B E$.
(1) 请判断直线 DE 与 $\odot O$ 的位置关系, 并证明你的结论;
(2) 若四边形 $A B C D$ 是正方形, 连接 $A C$, 当 $P$ 与 $C$ 重合时, 或当 $P$ 与 $B$ 重合时, 把 $\frac{P A+P C}{P D}$ 转化为正方形 $A B C D$ 的有关设段长的比, 可得 $\frac{P A+P C}{P D}=\sqrt{2}$ 是否成立? 请证明你的结论。
已知抛物线 $y=-x^2-\sqrt{3} x+c$ 经过点 $(0,2)$, 且与 $x$ 轴交于 $\mathrm{A} 、 \mathrm{~B}$ 两点. 设 $\mathrm{k}$ 是抛物线 $y=-x^2-\sqrt{3} x+c$ 与 $x$ 轴交点的横坐标; $\mathrm{M}$ 是抛物线 $y=-x^2-\sqrt{3} x+c$ 的 点, 常数 $m>0, S$ 为 $\triangle A B M$ 的面积. 已知使 $S=m$ 成立的点 $M$ 恰好有三个, 设 $T$ 为这三个点的纵坐标的和。
(1) 求 $\mathrm{c}$ 的值;
(2) 且接写出 $\mathrm{T}$ 的值;
(3) 求 $\frac{k^4}{k^8+k^6+2 k^4+4 k^2+16}$ 的值.