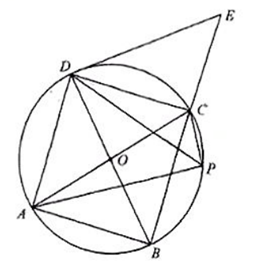
如图, 四边形 $A B C D$ 的外接圆是以 $B D$ 为直径的 $\odot O, P$ 是 $\odot O$ 的劣狐 $B C$ 上 的任 $E$ 意一点连接 $P A 、 P C 、 P D$, 延长 $B C$ 至 $E$, 使 $B D^2=B C \cdot B E$.
(1) 请判断直线 DE 与 $\odot O$ 的位置关系, 并证明你的结论;
(2) 若四边形 $A B C D$ 是正方形, 连接 $A C$, 当 $P$ 与 $C$ 重合时, 或当 $P$ 与 $B$ 重合时, 把 $\frac{P A+P C}{P D}$ 转化为正方形 $A B C D$ 的有关设段长的比, 可得 $\frac{P A+P C}{P D}=\sqrt{2}$ 是否成立? 请证明你的结论。