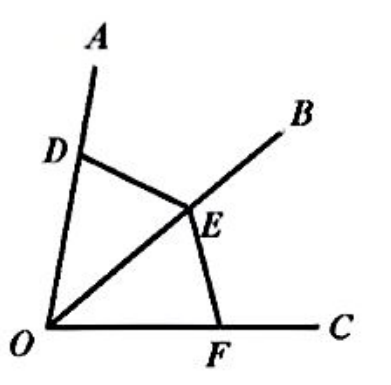
如图, $O B$ 平分 $\angle A O C, D 、 E 、 F$ 分别是射线 $O A$ 、射线 $O B 、$ 射线 $O C$ 上的点, $D 、 E 、 F$ 与 $O$ 点都不重合, 连接 $E D 、 E F$ 若添加下列条件中的某一个.就能使 $\triangle D O E$ $\cong \triangle \mathrm{FOE}$, 你认为要添加的那个条件是
$\text{A.}$ $\mathrm{OD}=\mathrm{OE}$
$\text{B.}$ $\mathrm{OE}=\mathrm{OF}$
$\text{C.}$ $\angle \mathrm{ODE}=\angle \mathrm{OED}$
$\text{D.}$ $\angle \mathrm{ODE}=\angle \mathrm{OFE}$