单选题 (共 12 题 ),每题只有一个选项正确
若 $2^4 \times 2^2=2^m$, 则 $m$ 的值为
$\text{A.}$ 8
$\text{B.}$ 6
$\text{C.}$ 5
$\text{D.}$ 2
若 $a, b$ 互为相反数, $c$ 的倒数是 4 , 则 $3 a+3 b-4 c$ 的值为
$\text{A.}$ $-8$
$\text{B.}$ $-5$
$\text{C.}$ $-1$
$\text{D.}$ $16$
若 $m>n$, 则下列不等式中正确的是
$\text{A.}$ $m-2 < n-2$
$\text{B.}$ $-\frac{1}{2} m>-\frac{1}{2} n$
$\text{C.}$ $n-m>0$
$\text{D.}$ $1-2 m < 1-2 n$
几个大小相同, 且棱长为 1 的小正方体所搭成几何体的俯视图如图 1 所示, 图中小正 方形中的数字表示在该位置小正方体的个数, 则这个几何体的左视图的面积为
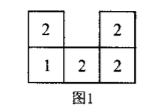
$\text{A.}$ 3
$\text{B.}$ 4
$\text{C.}$ 6
$\text{D.}$ 9
2022 年 2 月 20 日北京冬奥会大幕落下, 中国队在冰上、雪上项目中, 共斩获 9 金 4 银 2 铜, 创造中国队冬奥会历史最好成绩. 某校为普及冬奥知识, 开展了校内冬奥知识竞 赛活动, 并评出一等奖 3 人. 现欲从小明等 3 名一等奖获得者中任选 2 名参加全市冬奥 知识竞赛, 则小明被选到的概率为
$\text{A.}$ $\frac{1}{6}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{2}{3}$
若 $x_1, x_2$ 是方程 $x^2-2 x-3=0$ 的两个实数根, 则 $x_1 \cdot x_2^2$ 的值为
$\text{A.}$ 3 或 $-9$
$\text{B.}$ $-3$ 或 9
$\text{C.}$ 3 或 $-6$
$\text{D.}$ $-3$ 或 6
如图 2, $A B, C D$ 是 $\odot O$ 的两条直径, $E$ 是劣弧 $\widehat{B C}$ 的中点, 连接 $B C$, $D E$. 若 $\angle A B C=22^{\circ}$, 则 $\angle C D E$ 的度数为
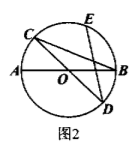
$\text{A.}$ $22^{\circ}$
$\text{B.}$ $32^{\circ}$
$\text{C.}$ $34^{\circ}$
$\text{D.}$ $44^{\circ}$
在一次函数 $y=-5 a x+b(a \neq 0)$ 中, $y$ 的值随 $x$ 值的增大而增大, 且 $a b>0$, 则点 $A(a, b)$ 在
$\text{A.}$ 第四象限
$\text{B.}$ 第三象限
$\text{C.}$ 第二象限
$\text{D.}$ 第一象限
如图 3, 在边长为 1 的小正方形组成的网格中, $A, B, C, D$ 四个点 均在格点上, $A C$ 与 $B D$ 相交于点 $E$, 连接 $A B, C D$, 则 $\triangle A B E$ 与 $\triangle C D E$ 的周长比为
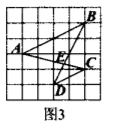
$\text{A.}$ $1: 4$
$\text{B.}$ $4: 1$
$\text{C.}$ $1: 2$
$\text{D.}$ $2: 1$
已知实数 $a, b$ 满足 $b-a=1$, 则代数式 $a^2+2 b-6 a+7$ 的最小值等于
$\text{A.}$ 5
$\text{B.}$ 4
$\text{C.}$ 3
$\text{D.}$ 2
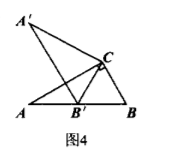
如图 4, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, \angle A=30^{\circ}, B C=2$, 将 $\triangle A B C$ 绕点 $C$ 顺时针旋转得到 $\triangle A^{\prime} B^{\prime} C$, 其中点 $A^{\prime}$ 与点 $A$ 是对应点, 点 $B^{\prime}$ 与点 $B$ 是对应点.若点 $B^{\prime}$ 恰好落在 $A B$ 边上, 则点 $A$ 到直线 $A^{\prime} C$ 的 距离等于
$\text{A.}$ $3 \sqrt{3}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ $3$
$\text{D.}$ $2$
如图 5, 在矩形 $A B C D$ 中, $A D>A B$, 点 $E, F$ 分别在 $A D, B C$ 边上, $E F / / A B, A E=A B, A F$ 与 $B E$ 相交于点 $O$, 连接 $O C$. 若 $B F=2 C F$, 则 $O C$ 与 $E F$ 之间的数量关系正确的是
$\text{A.}$ $2 O C=\sqrt{5} E F$
$\text{B.}$ $\sqrt{5} O C=2 E F$
$\text{C.}$ $2 O C=\sqrt{3} E F$
$\text{D.}$ $O C=E F$
填空题 (共 7 题 ),请把答案直接填写在答题纸上
若代数式 $\sqrt{x+1}+\frac{1}{x}$ 在实数范围内有意义, 则 $x$ 的取值范围是
计算: $\frac{a^2}{a-b}+\frac{b^2-2 a b}{a-b}=$
某校欲招聘一名教师, 对甲、乙两名候选人进行了三项素质测试, 各项测试成绩满分 均为 100 分, 根据最终成绩择优录用, 他们的各项测试成绩如下表所示:
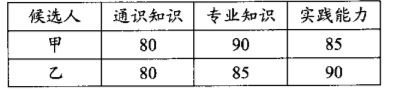
根据实际需要, 学校将通识知识、专业知识和实践能力三项测试得分按 $2: 5: 3$ 的比例
确定每人的最终成绩, 此时被录用的是
(填“甲”或“乙”)
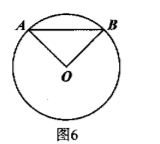
如图 6, 已知 $\odot O$ 的半径为 $2, A B$ 是 $\odot O$ 的弦若 $A B=2 \sqrt{2}$, 则劣弧 $\widehat{A B}$ 的长为
若一个多项式加上 $3 x y+2 y^2-8$, 结果得 $2 x y+3 y^2-5$, 则这个多项式 为
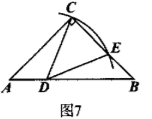
如图 7, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, A C=B C=3, D$ 为 $A B$ 边 上一点, 且 $B D=B C$, 连接 $C D$, 以点 $D$ 为圆心, $D C$ 的长为半径 作弧, 交 $B C$ 于点 $E$ (异于点 $C$ ), 连接 $D E$, 则 $B E$ 的长为
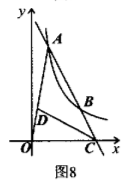
如图 8, 反比例函数 $y=\frac{k}{x}(k>0)$ 在第一象限的图象上有 $A(1,6)$,
$B(3, b)$ 两点, 直线 $A B$ 与 $x$ 轴相交于点 $C, D$ 是线段 $O A$ 上一点. 若 $A D \cdot B C=A B \cdot D O$, 连接 $C D$, 记 $\triangle A D C, \triangle D O C$ 的面积分别 为 $S_1, S_2$, 则 $S_1-S_2$ 的值为
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
2022 年 3 月 28 日是第 27 个全国中小学生安全教育日. 某校为调查本校学生对安全知 识的了解情况, 从全校学生中随机抽取若干名学生进行测试, 测试后发现所有测试的学生 成绩均不低于 50 分:将全部测试成绩 $x$ (单位: 分) 进行整理后分为五组 $(50 \leqslant x < 60$, $60 \leqslant x < 70,70 \leqslant x < 80,80 \leqslant x < 90,90 \leqslant x \leqslant 100$ ), 并绘制成如下的频数直方图 (如图 9).
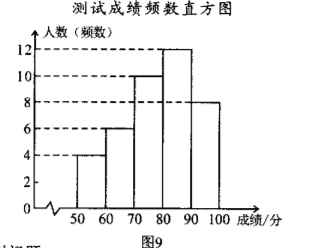
请根据所给信息, 解答下列问题:
(1)在这次调查中,一共抽取了 名学生;
(2)若测试成绩达到 80 分及以上为优秀, 请你估计全校 960 名学生对安全知识的了 解情况为优秀的学生人数;
(3) 为了进一步做好学生安全教育工作, 根据调查结果, 请你为学校提一条合理化建 议.
如图 $10, A B$ 是底部 $B$ 不可到达的一座建筑物, $A$ 为建筑物的最高点, 测角仪器的高 $D H=C G=1.5$ 米.某数学兴趣小组为测量建筑物 $A B$ 的高度, 先在 $H$ 处用测角仪器测得建筑物 顶端 $A$ 处的仰角 $\angle A D E$ 为 $\alpha$, 再向前走 5 米到达 $G$ 处, 又测得建筑物顶端 $A$ 处的仰角 $\angle A C E$ 为 $45^{\circ}$, 已知 $\tan \alpha=\frac{7}{9}, A B \perp B H, H, G, B$ 三点在同一水平线上, 求建筑物 $A B$ 的高度.

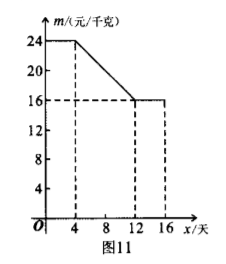
由于精准扶贫的措施科学得当, 贫困户小颖家今年种植的草苺喜获丰收, 采摘上市 16 天全部销售完.小颖对销售情况进行统计后发现, 在该草莓上市第 $x$ 天 ( $x$ 取整数) 时, 日销售量 $y$ (单位: 千克) 与 $x$ 之间的函数关系式为 $y= \begin{cases}12 x, & 0 \leqslant x \leqslant 10, \\ -20 x+320, & 10 < x \leqslant 16,\end{cases}$
草苺价格 $m$ (单位: 元/千克) 与 $x$ 之间的函数关系如图 11 所示.
(1) 求第 14 天小颌家草䔦的日销售量;
(2) 求当 $4 \leqslant x \leqslant 12$ 时, 草苺价格 $m$ 与 $x$ 之间的函数关系式;
(3)试比较第 8 天与第 10 天的销售金额哪天多?
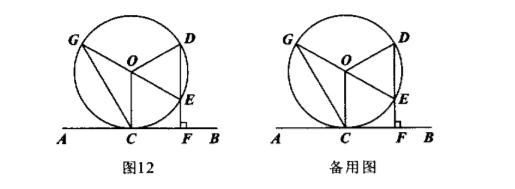
如图 12, $A B$ 为 $\odot O$ 的切线, $C$ 为切点, $D$ 是 $\odot O$ 上一点, 过点 $D$ 作 $D F \perp A B$, 垂足 为 $F, D F$ 交 $\odot O$ 于点 $E$, 连接 $E O$ 并延长交 $\odot O$ 于点 $G$, 连接 $C G, O C, O D$, 已知 $\angle D O E=2 \angle C G E$.
(1) 若 $\odot O$ 的半径为 5 , 求 $C G$ 的长;
(2) 试探究 $D E$ 与 $E F$ 之间的数量关系, 写出并证明你的结论. (请用两种证法解答)
如图13,在平行四边形ABCD中,AC是一条对角线,且$AB=AC=5,BC=6$,$E,F$是$AD$边上两点, 点 $F$ 在点 $E$ 的右侧, $A E=D F$, 连接 $C E, C E$ 的延长线与 $B A$ 的延长线相交于点 $G$.
(1) 如图 13-1, $M$ 是 $B C$ 边上一点, 连接 $A M, M F, M F$ 与 $C E$ 相交于点 $N$.
(1) 若 $A E=\frac{3}{2}$, 求 $A G$ 的长;
(2)在满足(1)的条件下, 若 $E N=N C$, 求证: $A M \perp B C$;
(2) 如图 13-2, 连接 $G F, H$ 是 $G F$ 上一点, 连接 $E H$. 若 $\angle E H G=\angle E F G+\angle C E F$, 且 $H F=2 G H$, 求 $E F$ 的长.

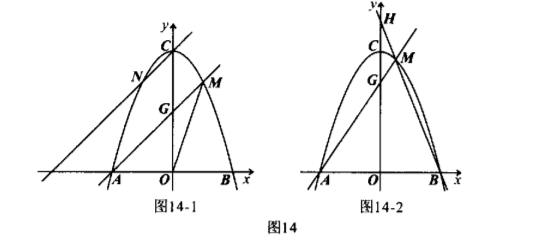
如图 14, 在平面直角坐标系中, 抛物线 $y=a x^2+c(a \neq 0)$ 与 $x$ 轴交于 $A, B$ 两点, 点 $B$ 的 坐标是 $(2,0)$, 顶点 $C$ 的坐标是 $(0,4), M$ 是抛物线上一动点, 且位于第一象限, 直线 $A M$ 与 $y$ 轴交于点 $G$.
(1)求该抛物线的解析式;
(2) 如图 14-1, $N$ 是抛物线上一点, 且位于第二象限, 连接 $O M$, 记 $\triangle A O G, \triangle M O G$ 的面积分别为 $S_1, S_2$. 当 $S_1=2 S_2$, 且直线 $C N / / A M$ 时, 求证: 点 $N$ 与点 $M$ 关于 $y$ 轴对称;
(3) 如图 14-2, 直线 $B M$ 与 $y$ 轴交于点 $H$, 是否存在点 $M$, 使得 $2 O H-O G=7$. 若 存在, 求出点 $M$ 的坐标; 若不存在, 请说明理由.