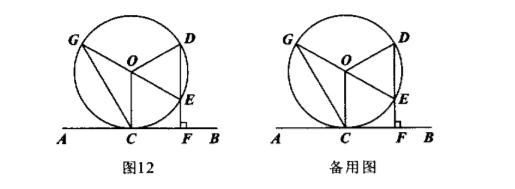
如图 12, $A B$ 为 $\odot O$ 的切线, $C$ 为切点, $D$ 是 $\odot O$ 上一点, 过点 $D$ 作 $D F \perp A B$, 垂足 为 $F, D F$ 交 $\odot O$ 于点 $E$, 连接 $E O$ 并延长交 $\odot O$ 于点 $G$, 连接 $C G, O C, O D$, 已知 $\angle D O E=2 \angle C G E$.
(1) 若 $\odot O$ 的半径为 5 , 求 $C G$ 的长;
(2) 试探究 $D E$ 与 $E F$ 之间的数量关系, 写出并证明你的结论. (请用两种证法解答)