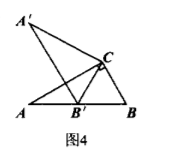
如图 4, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, \angle A=30^{\circ}, B C=2$, 将 $\triangle A B C$ 绕点 $C$ 顺时针旋转得到 $\triangle A^{\prime} B^{\prime} C$, 其中点 $A^{\prime}$ 与点 $A$ 是对应点, 点 $B^{\prime}$ 与点 $B$ 是对应点.若点 $B^{\prime}$ 恰好落在 $A B$ 边上, 则点 $A$ 到直线 $A^{\prime} C$ 的 距离等于
$\text{A.}$ $3 \sqrt{3}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ $3$
$\text{D.}$ $2$