单选题 (共 8 题 ),每题只有一个选项正确
设集合 $A=\{x \mid-1 < x < 1\}, B=\left\{x \mid x^2-2 x \leq 0\right\}$, 则 $A \cup B=$ ()
$\text{A.}$ $(-1,2]$
$\text{B.}$ $(-1,2)$
$\text{C.}$ $[0,1)$
$\text{D.}$ $(0,1]$
已知 $\mathrm{i}$ 为虚数单位, 复数 $z$ 满足 $z(1+\mathrm{i})=4-3 \mathrm{i}$, 则复数 $z$ 在复平面内对应的点位于()
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
设向量 $\vec{a}, \vec{b}$ 是互相垂直的单位向量, 则与向量 $\vec{a}-\vec{b}$ 垂直的一个单位向量是()
$\text{A.}$ $\vec{a}+\vec{b}$
$\text{B.}$ $\frac{\sqrt{5}}{5}(\vec{a}-2 \vec{b})$
$\text{C.}$ $\frac{\sqrt{2}}{2}(-\vec{a}-\vec{b})$
$\text{D.}$ $\frac{\sqrt{5}}{5}(\vec{a}+2 \vec{b})$
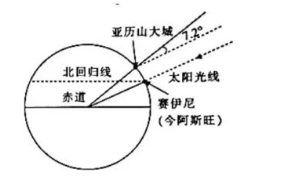
埃拉托斯特尼是古希腊亚历山大时期著名的地理学家, 他最出名的工作是计算了地球(大圆)的周长.如图, 在赛伊尼,夏至那天中午的太阳几乎正在天顶方向(这是从日光直射进该处一井内而得到证明的).同时在亚 历山大城(该处与赛伊尼几乎在同一子午线上), 其天顶方向与太阳光线的夹角测得为 $7.2^{\circ}$. 因太阳距离地球很 远, 故可把太阳光线看成是平行的.埃拉托斯特尼从商队那里知道两个城市间的实际距离大概是 5000 斯塔蒂亚, 按埃及的长度算, 1 斯塔蒂亚等于 $157.5$ 米, 则埃拉托斯特尼所测得地球的周长约为()
$\text{A.}$ 38680 千米
$\text{B.}$ 39375 千米
$\text{C.}$ 41200 千米
$\text{D.}$ 42192 千米
已知关于 $x$ 的不等式 $a x^2+b x+4>0$ 的解集为 $(-\infty, m) \cup\left(\frac{4}{m},+\infty\right)$, 其中 $m < 0$, 则 $\frac{b}{a}+\frac{4}{b}$ 的最小值为 ( )
$\text{A.}$ $-4$
$\text{B.}$ $4$
$\text{C.}$ $5$
$\text{D.}$ $8$
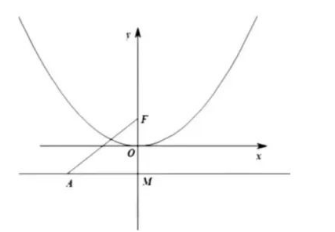
在平面直角坐标系 $x O y$ 中, 设抛物线 $x^2=4 y$ 的焦点为 $F$, 准线为 $l, P$ 为抛物线上一点, 过点 $P$ 作 $P A \perp l$, 交准线 $l$ 于点 $A$, 若直线 $A F$ 的倾斜角为 $30^{\circ}$, 则点 $P$ 的纵坐标为()
$\text{A.}$ 3
$\text{B.}$ 2
$\text{C.}$ 1
$\text{D.}$ $\frac{1}{2}$
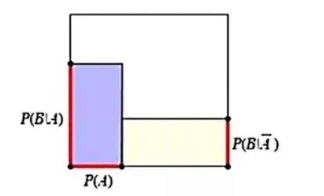
若将整个样本空间想象成一个 $1 \times 1$ 的正方形, 任何事件都对应样本空间的一个子集, 且事件发生的概率对 应子集的面积, 则如图所示的涂色部分的面积表示
$\text{A.}$ 事件 $A$ 发生的概率
$\text{B.}$ 事件 $B$ 发生的概率
$\text{C.}$ 事件 $B$ 不发生条件下事件 $A$ 发生的概率
$\text{D.}$ 事件 $A, B$ 同时发生的概率
已知 $a=\sin 0.1, b=\ln 1.1, c=e^{0.1}-1$, 则
$\text{A.}$ $c < b < a$
$\text{B.}$ $a < b < c$
$\text{C.}$ $c < a < b$
$\text{D.}$ $b < a < c$
多选题 (共 4 题 ),每题有多个选项正确
下列说法正确的有()
$\text{A.}$ 已知一组数据 $7,7,8,9,5,6,8,8$, 则这组数据的中位数为 8
$\text{B.}$ 已知一组数据 $x_1, x_2, x_3, \ldots, x_{10}$ 的方差为 2 , 则 $x_1+2, x_2+2, x_3+2, \ldots, x_{10}+2$ 的方差为 2
$\text{C.}$ 具有线性相关关系的变量 $x, y$, 其线性回归方程为 $\hat{y}=0.2 x-m$, 若样本点的中心为 $(m, 3.2)$, 则 $m=4$
$\text{D.}$ 若随机变量 $X$ 服从正态分布 $N\left(2, \sigma^2\right), P(X \leq 3)=0.64$, 则 $P(1 \leq X \leq 2)=0.14$
已知函数 $f(x)=\sin \omega x+\cos \omega x(\omega>0)$ 图象的相邻两条对称轴之间的距离为 $\frac{\pi}{2}$, 则()
$\text{A.}$ $f(x)$ 的图象关于点 $\left(\frac{3 \pi}{8}, 0\right)$ 对称
$\text{B.}$ 将 $f(x)$ 的图象向左平移 $\frac{\pi}{8}$ 个单位长度, 得到的函数图象关于 $y$ 轴对称
$\text{C.}$ $f(x)$ 在 $\left[0, \frac{\pi}{2}\right]$ 上的值域为 $[-1,1]$
$\text{D.}$ $f(x)$ 在 $\left[-\frac{\pi}{4}, 0\right]$ 上单调递增
在棱长为 2 的正方体 $A B C D-A_1 B_1 C_1 D_1$ 中, 点 $M, N$ 分别是棱 $A_1 D_1, A B$ 的中点, 则
$\text{A.}$ 异面直线 $M D$ 与 $A C$ 所成角的余弦值为 $\frac{1}{5}$
$\text{B.}$ $M C_1 \perp D_1 N$
$\text{C.}$ 四面体 $C A B_1 D_1$ 的外接球体积为 $4 \sqrt{3} \pi$
$\text{D.}$ 平面 $M N C$ 截正方体所得的截面是四边形
已知 $S_n$ 是数列 $\left\{a_n\right\}$ 的前 $n$ 项和, $S_{n+1}=-S_n+n^2$, 则 ( )
$\text{A.}$ $a_n+a_{n+1}=2 n-1(n \geq 2)$
$\text{B.}$ $a_{n+2}-a_n=2$
$\text{C.}$ 当 $a_1=0$ 时, $S_{50}=1225$
$\text{D.}$ 当数列 $\left\{a_n\right\}$ 单调递增时, $a_1$ 的取值范围是 $\left(-\frac{1}{4}, \frac{1}{4}\right)$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
$\left(1+\frac{1}{x^2}\right)(1+x)^6$ 展开式中 $x^3$ 的系数为
已知角 $a$ 的顶点在坐标原点 $O$, 始边与 $x$ 轴的非负半轴重合, 将角 $a$ 的终边绕 $O$ 点逆时针旋转 $\frac{\pi}{12}$ 后, 经 过点 $(1,-3)$, 则 $\cos \left(a+\frac{\pi}{3}\right)=$
已知函数 $f(x)=\left\{\begin{array}{l}x^2-3 x+2, x \geq 0 \\ |x+2|, x < 0\end{array}, g(x)=k x+1\right.$. 若函数 $h(x)=f(x)-g(x)$ 的图象经过四个象限, 则实数 $k$ 的取值范围是
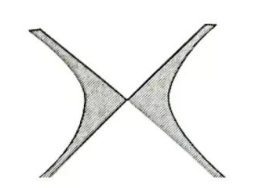
祖晅是我国南北朝时期伟大的数学家, 他于 5 世纪末提出了“幂势既同, 则积不容异”的体积计算原理, 即“夹 在两个平行平面之间的两个几何体, 被平行于这两个平而的任意平面所截, 如果截得的两个截面的面积总相等, 那么这两个几何体的体积相等". 现已知直线 $y=\pm 2$ 与双曲线 $x^2-y^2=4$ 及其渐近线围成的平面图形 $G$ 如图 所示.若将图形 $G$ 被直线 $y=t(-2 \leq t \leq 2)$ 所截得的两条线段绕 $y$ 轴旋转一周, 则形成的旋转面的面积 $S=$ ; 若将图形 $G$ 绕 $y$ 轴旋转一周, 则形成的旋转体的体积 $V=$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
从 ①$(3 n-1) a_{n+1}=(3 n+2) a_n$, ② $a_2=5,2 a_{n+1}=a_n+a_{n+2}$ 这两个条件中任选一个, 补充在下面的问题中并 作答.
已知数列 $\left\{a_n\right\}$ 满足 $a_1=2$,
(1) 求 $\left\{a_n\right\}$ 的通项公式;
(2) 设 $b_n=\left(\frac{1}{2}\right)^{a_n}$, 求数列 $\left\{a_n+b_n\right\}$ 的前 $n$ 项和 $T_n$.
注: 若选两个条件分别作答, 则按第一个解答计分.
在 $\triangle A B C$ 中, 内角 $A, B, C$ 的对边分别为 $a, b, c$, 且 $B=\frac{2 \pi}{3}, b=\sqrt{6}$.
(1)若 $\triangle A B C$ 的周长为 $2 \sqrt{2}+\sqrt{6}$, 求 $a, c$ 的值;
(2)若 $\triangle A B C$ 的面积为 $\frac{\sqrt{3}}{3}$, 求 $\sin A \sin C$ 的值.
近年来, 师范专业是高考考生填报志愿的热门专业.某高中随机调查了本校 2022 年参加高考的 90 位文科考生首 选志愿(第一个院校专业组的第一个专业)填报情况,经统计,首选志愿填报与性别情况如下表:(单位:人)

(1)根据表中数据.能否有 $95 \%$ 的把握认为首选志愿为师范专业与性别有关?
(2)用样本估计总体, 用本次调研中首选志愿样本的频率代替首选志愿的概率, 从 2022 年全国文科考生中随 机抽取 3 人, 设被抽取的 3 人中首选志愿为师范专业的人数为 $X$, 求 $X$ 的分布列、数学期望 $E(X)$ 和方差 $D(X)$.
附: $\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}, \quad n=a+b+c+d$.

在四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 为直角梯形, $A D \| B C, A D \perp A B$, 侧面 $P A B \perp$ 底面 $A B C D$, $P A=P B=A D=\frac{1}{2} B C=2$, 且 $E, F$ 分别为 $P C, C D$ 的中点.
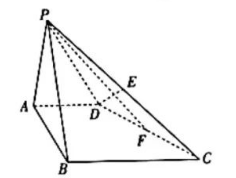
(1) 证明: $D E$ I 平面 $P A B$.
(2) 若直线 $P F$ 与平面 $P A B$ 所成的角为 $60^{\circ}$, 求平面 $P A B$ 与平面 $P C D$ 所成锐二面角的余弦值.
设 $F$ 为椭圆 $C: \frac{x^2}{2}+y^2=1$ 的右焦点,过点 $F$ 且与 $x$ 轴不重合的直线 $l$ 交椭圆 $C$ 于 $A, B$ 两点.
(1) 当 $\overrightarrow{B F}=2 \overrightarrow{F A}$ 时, 求 $|\overrightarrow{F A}|$;
(2) 在 $x$ 轴上是否存在异于 $F$ 的定点 $Q$, 使 $\frac{k_{Q A}}{k_{Q B}}$ 为定值 (其中 $k_{Q A}, k_{Q B}$ 分别为直线 $Q A, Q B$ 的斜率)? 若 存在, 求出 $Q$ 的坐标; 若不存在, 请说明理由.
已知函数 $f(x)=2 e^{x-1}-a(x-\ln x-1)-2 x, x \in(1,+\infty)$.
(1) 当 $a=0$ 时, 求曲线 $y=f(x)$ 在 $x=2$ 处的切线方程;
(2) 若 $f(x)>0$, 求实数 $a$ 的取值范围.