在四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 为直角梯形, $A D \| B C, A D \perp A B$, 侧面 $P A B \perp$ 底面 $A B C D$, $P A=P B=A D=\frac{1}{2} B C=2$, 且 $E, F$ 分别为 $P C, C D$ 的中点.


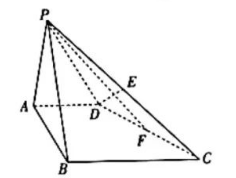
(1) 证明: $D E$ I 平面 $P A B$.
(2) 若直线 $P F$ 与平面 $P A B$ 所成的角为 $60^{\circ}$, 求平面 $P A B$ 与平面 $P C D$ 所成锐二面角的余弦值.