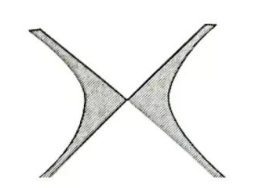
祖晅是我国南北朝时期伟大的数学家, 他于 5 世纪末提出了“幂势既同, 则积不容异”的体积计算原理, 即“夹 在两个平行平面之间的两个几何体, 被平行于这两个平而的任意平面所截, 如果截得的两个截面的面积总相等, 那么这两个几何体的体积相等". 现已知直线 $y=\pm 2$ 与双曲线 $x^2-y^2=4$ 及其渐近线围成的平面图形 $G$ 如图 所示.若将图形 $G$ 被直线 $y=t(-2 \leq t \leq 2)$ 所截得的两条线段绕 $y$ 轴旋转一周, 则形成的旋转面的面积 $S=$ ; 若将图形 $G$ 绕 $y$ 轴旋转一周, 则形成的旋转体的体积 $V=$