单选题 （共 8 题 ），每题只有一个选项正确
截至 2023 年 6 月 11 日 17 时, 全国冬小麦收款 2.39 亿亩, 进度过七成半, 将 239000000 用科学记数法 表示应为
$\text{A.}$ $23.9 \times 10^7$
$\text{B.}$ $2.39 \times 10^8$
$\text{C.}$ $2.39 \times 10^9$
$\text{D.}$ $0.239 \times 10^9$
下列图形中, 既是轴对称图形又是中心对称图形的是
$\text{A.}$ 
$\text{B.}$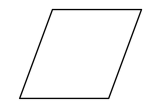 
$\text{C.}$ 
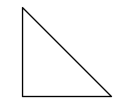$\text{D.}$ 
如图, $\angle A O C=\angle B O D=90^{\circ}, \angle A O D=126^{\circ}$, 则 $\angle B O C$ 的大小为
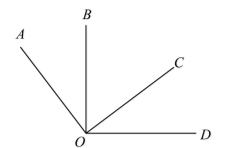
$\text{A.}$ $36^{\circ}$
$\text{B.}$ $44^{\circ}$
$\text{C.}$ $54^{\circ}$
$\text{D.}$ $63^{\circ}$
已知 $a-1>0$, 则下列结论正确的是
$\text{A.}$ $-1 < -a < a < 1$
$\text{B.}$ $-a < -1 < 1 < a$
$\text{C.}$ $-a < -1 < a < 1$
$\text{D.}$ $-1 < -a < 1 < a$
若关于 $x$ 的一元二次方程 $x^2-3 x+m=0$ 有两个相等的实数根, 则实数 $m$ 的值为
$\text{A.}$ -9
$\text{B.}$ $-\frac{9}{4}$
$\text{C.}$ $\frac{9}{4}$
$\text{D.}$ 9
十二边形的外角和为
$\text{A.}$ $30^{\circ}$
$\text{B.}$ $150^{\circ}$
$\text{C.}$ $360^{\circ}$
$\text{D.}$ $1800^{\circ}$
先后两次抛掷同一枚质地均匀的硬币, 则第一次正面向上、第二次反面向上的概率是
$\text{A.}$ $\frac{1}{4}$
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{3}{4}$
如图, 点 $\mathrm{A} 、 \mathrm{~B} 、 \mathrm{C}$ 在同一条线上, 点 $\mathrm{B}$ 在点 $\mathrm{A}, \mathrm{C}$ 之间, 点 $\mathrm{D}, \mathrm{E}$ 在直线 $\mathrm{AC}$ 同侧, $A B < B C, \angle A=\angle C=90^{\circ}$,
$\triangle E A B \cong \triangle B C D$, 连接 $\mathrm{DE}$, 设 $A B=a, B C=b, D E=c$, 给出下面三个结论:
(1) $a+b < c$;
(2) $a+b>\sqrt{a^2+b^2}$;
(3) $\sqrt{2}(a+b)>c$;
上述结论中, 所有正确结论的序号是
$\text{A.}$ (1)(2)
$\text{B.}$ (1) (3)
$\text{C.}$ (2)(3)
$\text{D.}$ (1) (2) (3)
填空题 （共 8 题 ），请把答案直接填写在答题纸上
若代数式 $\frac{5}{x-2}$ 有意义, 则实数 $\mathrm{x}$ 的取值范围是
方程 $\frac{3}{5 x+1}=\frac{1}{2 x}$ 的解为
在平面直角坐标系 $x O y$ 中, 若函数 $y=\frac{k}{x}(k \neq 0)$ 的图象经过点 $A(-3,2)$ 和 $B(m,-2)$, 则 $\mathrm{m}$ 的值 为
某厂生产了 1000 只灯泡. 为了解这 1000 只灯泡的使用寿命, 从中随机抽取了 50 只灯泡进行检测, 获得 了它们的使用寿命 (单位: 小时), 数据整理如下:
根据以上数据, 估计这 1000 只灯泡中使用寿命不小于 2200 小时的灯泡的数量为 ________ 只.
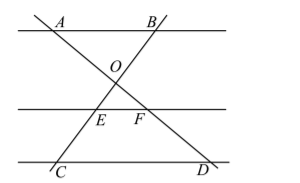
如图, 直线 $\mathrm{AD}, \mathrm{BC}$ 交于点 $\mathrm{O}, A B\|E F\| C D$. 若 $A O=2, O F=1, F D=2$. 则 $\frac{B E}{E C}$ 的值为
如图, $O A$ 是 $\odot O$ 的半径, $B C$ 是 $\odot O$ 的弦, $O A \perp B C$ 于点 $\mathrm{D}, A E$ 是 $\odot O$ 的切线, $A E$ 交 $O C$ 的延长线 于点 $\mathrm{E}$. 若 $\angle A O C=45^{\circ}, B C=2$, 则线段 $A E$ 的长为
学校组织学生参加木艺艺术品加工劳动实践活动. 已知某木艺艺术品加工完成共需 $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E}$, $F, G$ 七道工序, 加工要求如下:
(1)工序 C, D 须在工序 $\mathrm{A}$ 完成后进行, 工序 $\mathrm{E}$ 须在工序 $\mathrm{B}, \mathrm{D}$ 都完成后进行, 工序 $\mathrm{F}$ 须在工序 $\mathrm{C}, \mathrm{D}$ 都完 成后进行;
(2)一道工序只能由一名学生完成, 此工序完成后该学生才能进行其他工序;
(3)各道工序所需时间如下表所示:
在不考虑其他因素的前提下, 若由一名学生单独完成此木艺艺术品的加工, 则需要 分钟; 若由两 名学生合作完成此木艺艺术品的加工, 则最少需要 分钟.
解答题 （共 12 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $4 \sin 60^{\circ}+\left(\frac{1}{3}\right)^{-1}+|-2|-\sqrt{12}$.
解不等式组: $\left\{\begin{array}{c}x>\frac{x+2}{3} \\ 5 x-3 < 5+x\end{array}\right.$.
已知 $x+2 y-1=0$, 求代数式 $\frac{2 x+4 y}{x^2+4 x y+4 y^2}$ 的值.
如图, 在 $A B C D$ 中, 点 $\mathrm{E}, \mathrm{F}$ 分别在 $B C, A D$ 上, $B E=D F, A C=E F$.
(1) 求证: 四边形 $A E C F$ 是矩形;
(2) $A E=B E, A B=2, \tan \angle A C B=\frac{1}{2}$, 求 $B C$ 的长.
对联是中华传统文化的瑰宝, 对联装裱后, 如图所示, 上、下空白处分别称为天头和地头, 左、右空 白处统称为边. 一般情况下, 天头长与地头长的比是 6: 4 , 左、右边的宽相等, 均为天头长与地头长的和 的 $\frac{1}{10}$. 某人要装裱一副对联, 对联的长为 $100 \mathrm{~cm}$, 宽为 $27 \mathrm{~cm}$. 若要求装裱后的长是装裱后的宽的 4 倍, 求边的宽和天头长. (书法作品选自 《启功法书》)
在平面直角坐标系 $x O y$ 中, 函数 $y=k x+b(k \neq 0)$ 的图象经过点 $A(0,1)$ 和 $B(1,2)$, 与过点 $(0,4)$ 且平行于 $\mathrm{x}$ 轴的线交于点 $\mathrm{C}$.
(1) 求该函数的解析式及点 $\mathrm{C}$ 的坐标;
(2) 当 $x < 3$ 时, 对于 $\mathrm{x}$ 的每一个值, 函数 $y=\frac{2}{3} x+n$ 的值大于函数 $y=k x+b(k \neq 0)$ 的值且小于 4 , 直 接写出 $\mathrm{n}$ 的值.
某校舞蹈队共 16 名学生, 测量并获取了所有学生的身高 (单位: $\mathrm{cm}$ ), 数据整理如下:
a. 16 名学生的身高:
$161,162,162,164,165,165,165,166,166,167,168,168,170,172,172,175$
b. 16 名学生的身高的平均数、中位数、众数:
(1) 写出表中 $\mathrm{m}, \mathrm{n}$ 的值;
(2) 对于不同组的学生, 如果一组学生的身高的方差越小, 则认为该组舞台呈现效果越好. 据此推断: 在 下列两组学生中, 舞台呈现效果更好的是 (填“甲组”或“乙组”);
(3) 该舞蹈队要选五名学生参加比赛. 已确定三名学生参赛, 他们的身高分别为 $168,168,172$, 他们的 身高的方差为 $\frac{32}{9}$. 在选另外两名学生时, 首先要求所选的两名学生与已确定的三名学生所组成的五名学生 的身高的方差小于 $\frac{32}{9}$, 其次要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的平均数尽 可能大, 则选出的另外两名学生的身高分别为 和
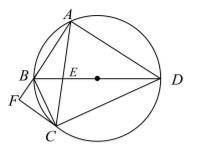
如图, 圆内接四边形 $A B C D$ 的对角线 $A C, B D$ 交于点 $E, B D$ 平分 $\angle A B C, \angle B A C=\angle A D B$.
(1) 求证 $D B$ 平分 $\angle A D C$, 并求 $\angle B A D$ 的大小;
(2) 过点 $C$ 作 $C F \| A D$ 交 $A B$ 的延长线于点 $F$. 若 $A C=A D, B F=2$, 求此圆半径的长.
某小组研究了清洗某种含污物品的节约用水策略. 部分内容如下.
每次清洗 1 个单位质量的该种含污物品, 清洗前的清洁度均为 0.800 要求清洗后的清洁度为 0.990 方案一: 采用一次清洗的方式.
结果: 当用水量为 19 个单位质量时, 清洗后测得的清洁度为 0.990 .
方案二: 采用两次清洗的方式.
记第一次用水量为 $x_1$ 个单位质量, 第二次用水量为 $x_2$ 个单位质量, 总用水量为 $\left(x_1+x_2\right)$ 个单位质量, 两 次清洗后测得的清洁度为 $\mathrm{C}$. 记录的部分实验数据如下:
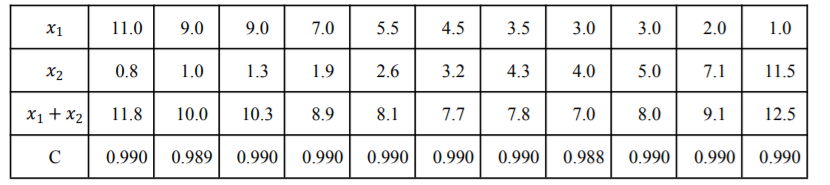
对以上实验数据进行分析, 补充完成以下内容.
(1) 选出 C 是 0.990 的所有数据组, 并划“ “ ”;
(2) 通过分析 (I) 中选出的数据, 发现可以用函数刻画第一次用水量 $x_1$ 和总用水量 $x_1+x_2$ 之间的关系, 在平面直角坐标系 $x O y$ 中画出此函数的图象;
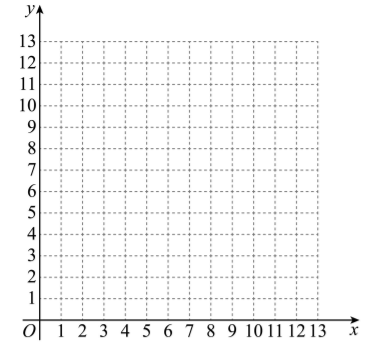
结果: 结合实验数据, 利用所画的函数图象可以推断, 当第一次用水量约为 个单 位质量（精确到个位）时, 总用水量最小.
(3) 根据以上实验数据和结果, 解决下列问题:
当采用两次清洗的方式并使总用水量最小时, 与采用一次清洗的方式相比、可节水约 个单位质 量 (结果保留小数点后一位);
(4) 当采用两次清洗的方式时, 若第一次用水量为 6 个单位质量, 总用水量为 7.5 个单位质量, 则清洗后 的清洁度 $\mathrm{C}$ 0.990 (填“>”“=”或“ $ < ”)$.
在平面直角坐标系 $x O y$ 中, $M\left(x_1, y_1\right), N\left(x_2, y_2\right)$ 是抛物线 $y=a x^2+b x+c(a>0)$ 上任意两点, 设 抛物线的对称轴为 $x=t$.
(1) 若对于 $x_1=1, x_2=2$ 有 $y_1=y_2$, 求 $t$ 的值;
(2) 若对于 $0 < x_1 < 1,1 < x_2 < 2$, 都有 $y_1 < y_2$, 求 $t$ 的取值范围.
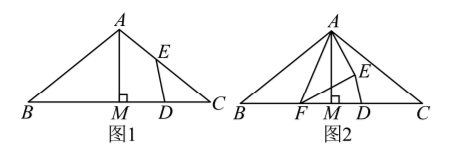
在 $\triangle A B C$ 中、 $\angle B=\angle C=\alpha\left(0^{\circ} < \alpha < 45^{\circ}\right), A M \perp B C$ 于点 $\mathrm{M}, \mathrm{D}$ 是线段 $M C$ 上的动点 (不与点 $\mathrm{M}, \mathrm{C}$ 重合), 将线段 $D M$ 绕点 $\mathrm{D}$ 顺时针旋转 $2 \alpha$ 得到线段 $D E$.
(1) 如图 1, 当点 $\mathrm{E}$ 在线段 $A C$ 上时, 求证: $\mathrm{D}$ 是 $M C$ 的中点;
(2) 如图 2, 若在线段 $B M$ 上存在点 $\mathrm{F}$ (不与点 $\mathrm{B}, \mathrm{M}$ 重合) 满足 $D F=D C$, 连接 $A E, E F$, 直接写出 $\angle A E F$ 的大小, 并证明.
在平面直角坐标系 $x O y$ 中, $\odot O$ 的半径为 1 . 对于 $\odot O$ 的弦 $A B$ 和 $\odot O$ 外一点 $\mathrm{C}$ 给出如下定义: 若直线 $C A, C B$ 中一条经过点 $\mathrm{O}$, 另一条是 $\odot O$ 的切线, 则称点 $\mathrm{C}$ 是弦 $A B$ 的“关联点”.
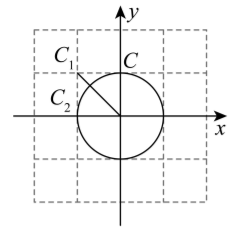
(1) 如图, 点 $A(-1,0), B_1\left(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right), B_2\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right)$
①在点 $C_1(-1,1), C_2(-\sqrt{2}, 0), C_3(0, \sqrt{2})$ 中, 弦 $A B_1$ 的“关联点”是 ________
② 若点 $\mathrm{C}$ 是弦 $A B_2$ 的“关联点”, 直接写出 $O C$ 的长;
（2）已知点 $M(0,3), N\left(\frac{6 \sqrt{5}}{5}, 0\right)$. 对于线段 $M N$ 上一点 $\mathrm{S}$, 存在 $\odot O$ 的弦 $P Q$, 使得点 $\mathrm{S}$ 是弦 $P Q$ 的“关 联点”, 记 $P Q$ 的长为 $\mathrm{t}$, 当点 $\mathrm{S}$ 在线段 $M N$ 上运动时, 直接写出 $\mathrm{t}$ 的取值范围.