在 $\triangle A B C$ 中、 $\angle B=\angle C=\alpha\left(0^{\circ} < \alpha < 45^{\circ}\right), A M \perp B C$ 于点 $\mathrm{M}, \mathrm{D}$ 是线段 $M C$ 上的动点 (不与点 $\mathrm{M}, \mathrm{C}$ 重合), 将线段 $D M$ 绕点 $\mathrm{D}$ 顺时针旋转 $2 \alpha$ 得到线段 $D E$.
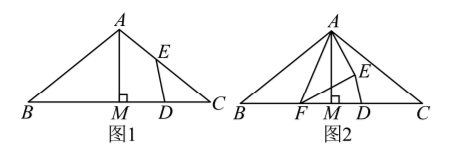
(1) 如图 1, 当点 $\mathrm{E}$ 在线段 $A C$ 上时, 求证: $\mathrm{D}$ 是 $M C$ 的中点;
(2) 如图 2, 若在线段 $B M$ 上存在点 $\mathrm{F}$ (不与点 $\mathrm{B}, \mathrm{M}$ 重合) 满足 $D F=D C$, 连接 $A E, E F$, 直接写出 $\angle A E F$ 的大小, 并证明.
(1) 如图 1, 当点 $\mathrm{E}$ 在线段 $A C$ 上时, 求证: $\mathrm{D}$ 是 $M C$ 的中点;
(2) 如图 2, 若在线段 $B M$ 上存在点 $\mathrm{F}$ (不与点 $\mathrm{B}, \mathrm{M}$ 重合) 满足 $D F=D C$, 连接 $A E, E F$, 直接写出 $\angle A E F$ 的大小, 并证明.
