在平面直角坐标系 $x O y$ 中, $\odot O$ 的半径为 1 . 对于 $\odot O$ 的弦 $A B$ 和 $\odot O$ 外一点 $\mathrm{C}$ 给出如下定义: 若直线 $C A, C B$ 中一条经过点 $\mathrm{O}$, 另一条是 $\odot O$ 的切线, 则称点 $\mathrm{C}$ 是弦 $A B$ 的“关联点”.

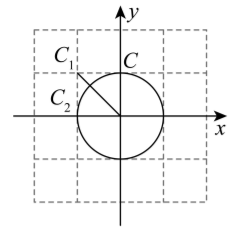
(1) 如图, 点 $A(-1,0), B_1\left(-\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right), B_2\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right)$
①在点 $C_1(-1,1), C_2(-\sqrt{2}, 0), C_3(0, \sqrt{2})$ 中, 弦 $A B_1$ 的“关联点”是 ________
② 若点 $\mathrm{C}$ 是弦 $A B_2$ 的“关联点”, 直接写出 $O C$ 的长;
（2）已知点 $M(0,3), N\left(\frac{6 \sqrt{5}}{5}, 0\right)$. 对于线段 $M N$ 上一点 $\mathrm{S}$, 存在 $\odot O$ 的弦 $P Q$, 使得点 $\mathrm{S}$ 是弦 $P Q$ 的“关 联点”, 记 $P Q$ 的长为 $\mathrm{t}$, 当点 $\mathrm{S}$ 在线段 $M N$ 上运动时, 直接写出 $\mathrm{t}$ 的取值范围.