单选题 （共 13 题 ），每题只有一个选项正确
若 $2^x-2^y < 3^{-x}-3^{-y}$ ，则
$\text{A.}$ $\ln (y-x+1)>0$
$\text{B.}$ $\ln (y-x+1) < 0$
$\text{C.}$ $\ln |x-y|>0$
$\text{D.}$ $\ln |x-y| < 0$
Logistic 模型是常用数学模型之一，可应用于流行病学领域。有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数 $I(t)\left(t\right.$ 的单位：天）的 Logistic 模型：$I(t)=\frac{K}{1+ e ^{-023(t-53)}}$ ，其中 $K$ 为最大确诊病例数．当 $I\left(t^*\right)=0.9$ $5 K$ 时，标志着已初步遏制疫情，则 $t^*$ 约为（ ）（ $\ln 19 \approx 3$ ）
$\text{A.}$ 60
$\text{B.}$ 63
$\text{C.}$ 66
$\text{D.}$ 69
基本再生数 $R_0$ 与世代间隔 $T$ 是新冠肺炎的流行病学基本参数。基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间．在新冠肺炎疫情初始阶段，可以用指数模型：$I(t)= e ^{r t}$ 描述累计感染病例数 $I(t)$ 随时间 $t$（单位：天）的变化规律，指数增长率 $r$ 与 $R_0, T$ 近似满足 $R_0=1+r T$ ．有学者基于已有数据估计出 $R_0=3.28, T=6$ ．据此，在新冠肺炎疫情初始阶段，累计感染病例数增加 1 倍需要的时间约为 $(\ln 2 \approx 0$ ．
$\text{A.}$ 1.2 天
$\text{B.}$ 1.8 天
$\text{C.}$ 2.5 天
$\text{D.}$ 3.5 天
设函数 $f(x)=\left\{\begin{array}{c}2^{-x}, x \leq 0 \\ 1, x>0\end{array}\right.$ ，则满足 $f(x+1) < f(2 x)$ 的 $x$ 的取值范围是
$\text{A.}$ $(-\infty,-1]$
$\text{B.}$ $(0,+\infty)$
$\text{C.}$ $(-1,0)$
$\text{D.}$ $(-\infty, 0)$
函数 $y=\left(3^x-3^{-x}\right) \cos x$ 在区间 $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ 的图象大致为
$\text{A.}$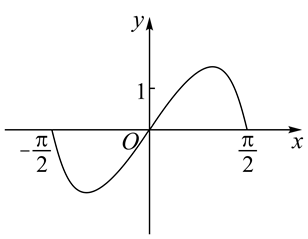 
$\text{B.}$ 
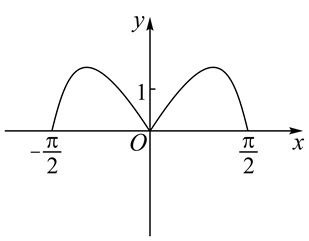$\text{C.}$ 
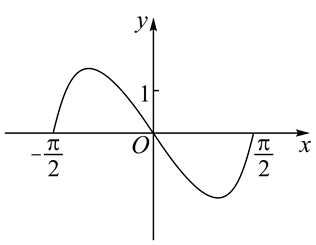$\text{D.}$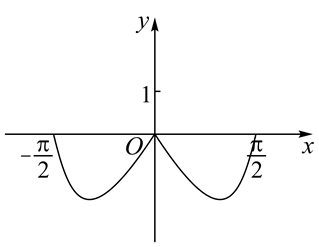 
已知 $a=2^{\frac{4}{3}}, b=4^{\frac{2}{5}}, c=5^{\frac{1}{3}}$ ，则（ ）
$\text{A.}$ $c < b < a$
$\text{B.}$ $a < b < c$
$\text{C.}$ $b < a < c$
$\text{D.}$ $c < a < b$
若函数 $f(x)=a^x-b$ 的图象如图所示，则
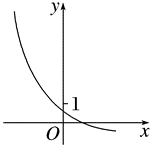
$\text{A.}$ $a>1, b>1$
$\text{B.}$ $a>1,0 < b < 1$
$\text{C.}$ $0 < a < 1, b>1$
$\text{D.}$ $0 < a < 1,0 < b < 1$
函数 $f(x)=a^x(a>0, a \neq 1)$ 在区间 $[1,2]$ 上的最大值是最小值的 2 倍，则 $a$ 的值是 $(\quad)$
$\text{A.}$ $\frac{1}{2}$ 或 $\sqrt{2}$
$\text{B.}$ $\frac{1}{2}$ 或 2
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ 2
已知定义在 $R$ 上的函数 $f(x)=2^{\left|x^{-} m\right|}-1(m$ 为实数 $)$ 为偶函数，记 $a=f\left(\log _{0.5} 3\right), b=f\left(\log _2 5\right), c=f(2 m)$ ，则 $a$ ， $b, c$ 的大小关系为（）
$\text{A.}$ $b < a < c$
$\text{B.}$ $c < a < b$
$\text{C.}$ $c < b < a$
$\text{D.}$ $a < b < c$ ．
如果函数 $y=a^{2 x}+2 a^x-1(a>0, a \neq 1)$ 在区间 $[-1,1]$ 上的最大值是 14 ，则 $a$ 的值为（ ）
$\text{A.}$ 3
$\text{B.}$ $\frac{1}{3}$
$\text{C.}$ -5
$\text{D.}$ 3 或 $\frac{1}{3}$ ．
已知函数 $f(x)=\ln (x-2)+\ln (4-x)$ ，则（ ）
$\text{A.}$ $f(x)$ 的图象关于直线 $x=3$ 对称
$\text{B.}$ $f(x)$ 的图象关于点 $(3,0)$ 对称
$\text{C.}$ $f(x)$ 在 $(2,4)$ 上单调递增
$\text{D.}$ $f(x)$ 在 $(2,4)$ 上单调递减
已知指数函数 $f(x)=a^x$ ，将函数 $f(x)$ 的图象上的每个点的横坐标不变，纵坐标扩大为原来的 3 倍，得到函数 $g(x)$ 的图象，再将 $g(x)$ 的图象向右平移 2 个单位长度，所得图象恰好与函数 $f(x)$ 的图象重合，则 $a$ 的值是（）
$\text{A.}$ $\frac{3}{2}$
$\text{B.}$ $\frac{2}{3}$
$\text{C.}$ $\frac{\sqrt{3}}{3}$
$\text{D.}$ $\sqrt{3}$
航天之父，俄罗斯科学家齐奥科夫斯基（K．E．Tsiolkovsky）于 1903 年给出火箭最大速度的计算公式 $v=V_0 \ln \left(1+\frac{M}{m_0}\right)$ ．其中，$V_0$ 是燃料相对于火箭的喷射速度，$M$ 是燃料的质量， $m_0$ 是火箭（除去燃料）的质量，$v$ 是火箭将燃料喷射完之后达到的速度．已知 $V_0=2 km / s$ ，则当火箭的最大速度 $v$ 可达到 $10 km / s$ 时，火箭的总质量（含燃料）至少是火箭（除去燃料）的质量的（ ）倍
$\text{A.}$ $e ^5$
$\text{B.}$ $e^5-1$
$\text{C.}$ $e ^6$
$\text{D.}$ $e^6-1$
多选题 （共 4 题 ），每题有多个选项正确
下列结论中，正确的是（ ）
$\text{A.}$ 函数 $y=2^{x-1}$ 是指数函数
$\text{B.}$ 函数 $y=a x^2+1(a>1)$ 的值域是 $[1,+\infty)$
$\text{C.}$ 若 $a^{m>a^n}(a>0, a \neq 1)$ ，则 $m>n$
$\text{D.}$ 函数 $f(x)=a^{x-2}-3(a>0, a \neq 1)$ 的图象必过点 $(2,-2)$
关于函数 $f(x)=\frac{1}{4^x+2}$ 的性质，下列说法中正确的是（ ）
$\text{A.}$ 函数 $f(x)$ 的定义域为 $R$
$\text{B.}$ 函数 $f(x)$ 的值域为 $(0,+\infty)$
$\text{C.}$ 方程 $f(x)=x$ 有且只有一个实根
$\text{D.}$ 函数 $f(x)$ 的图象是中心对称图形
已知 $f(x)$ 是定义在 $R$ 上的偶函数，且 $f(x+3)=f(x-1)$ ，若当 $x \in[0,2]$ 时，$f(x)=2^{x-1}$ ，则下列结论正确的是（ ）
$\text{A.}$ 当 $x \in[-2,0]$ 时，$f(x)=2^{-x}-1$
$\text{B.}$ $f(2019)=1$
$\text{C.}$ $y=f(x)$ 的图像关于点 $(2,0)$ 对称
$\text{D.}$ 函数 $g(x)=f(x)-\log _2 x$ 有 3 个零点
设 $a, b, c$ 都是正数，且 $4^a=6^b=9^c$ ，则下列结论正确的是（ ）
$\text{A.}$ $a b+b c=2 a c$
$\text{B.}$ $a b+b c=a c$
$\text{C.}$ $4^b \cdot 9^b=4^a \cdot 9^c$
$\text{D.}$ $\frac{1}{c}=\frac{2}{b}-\frac{1}{a}$
填空题 （共 1 题 ），请把答案直接填写在答题纸上
设函数 $f(x)$ 的定义域为 $R , f(x)$ 为偶函数，$f(x+1)$ 为奇函数，当 $x \in[1,2]$ 时，$f(x)=a \cdot 2^x+b$ ，若 $f(0)+f(1)=-4$ ，则 $f\left(\frac{7}{2}\right)=$
解答题 （共 2 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=2 a \cdot 4^x-2^x-1$ ．
（1）当 $a=1$ 时，求函数 $f(x)$ 在 $x \in[-3,0]$ 上的值域；
（2）若关于 $x$ 的方程 $f(x)=0$ 有解，求实数 $a$ 的取值范围．
已知函数 $f(x)=3^x+\lambda \cdot 3^{-x}(\lambda \in R )$ ．
（1）若 $f(x)$ 为奇函数，求 $\lambda$ 的值和此时不等式 $f(x)>1$ 的解集；
（2）若不等式 $f(x) \leqslant 6$ 对 $x \in[0,2]$ 恒成立，求实数 $\lambda$ 的取值范围．