单选题 (共 10 题 ),每题只有一个选项正确
下列各数中是无理数的是
$\text{A.}$ $0 . \dot{2} 0 \dot{3}$
$\text{B.}$ $-\sqrt[3]{27}$
$\text{C.}$ $\sqrt{4}$
$\text{D.}$ $0.1010010001 \cdots$ (每两个1之间增加一个 0$)$
下列各组数中, 是勾股数的是
$\text{A.}$ $1,1, \sqrt{2}$
$\text{B.}$ $9,12,15$
$\text{C.}$ $4,5,6$
$\text{D.}$ $1.5,2.5,2$
在平面直角坐标系中, 对于坐标 $P(3,4)$, 下列说法错误的是
$\text{A.}$ $P(3,4)$ 表示这个点在平面内的位置
$\text{B.}$ 点 $P$ 的纵坐标是 4
$\text{C.}$ 点 $P$ 到 $x$ 轴的距离是 4
$\text{D.}$ 它与点 $(4,3)$ 表示同一个坐标
$\sqrt{8}+1$ 的结果是介于下列哪两个数之间
$\text{A.}$ 2 和 3 之间
$\text{B.}$ 3 和4 之间
$\text{C.}$ 4 和5 之间
$\text{D.}$ 5 和 6之间
如果 $P(a, b)$ 在第三象限, 那么点 $Q(a+b, a b)$ 在
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
2021 年夏季郑州市强降雨高发, 新密市某村庄为缓解暴雨带来的洪灾问题, 在道路内侧新建了一 个排水渠排水 (横截面如图), 某天突发暴雨, 排水渠开始积水, 水位上涨, 暴雨停歇后, 排水渠 继续排水至积水全部排出, 假设排水速度为 $5 v$, 进水速度为 $7 v$, 下列图象中, 能反映以上过程排水 渠中水位高度 $h$ 与时间 $t$ 的关系的大致图象是
$\text{A.}$  $\text{B.}$
$\text{B.}$ 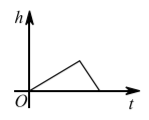 $\text{C.}$
$\text{C.}$ 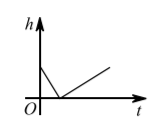 $\text{D.}$
$\text{D.}$ 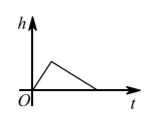
如图所示, 长方形纸片 $A B C D$ 中, $A B=4 \mathrm{~cm}, B C=8 \mathrm{~cm}$, 现将其沿 $E F$ 对折, 使得点 $C$ 与点 $A$ 重 合, 则 $A F$ 长为

$\text{A.}$ $3 \mathrm{~cm}$
$\text{B.}$ $\frac{12}{5} \mathrm{~cm}$
$\text{C.}$ $5 \mathrm{~cm}$
$\text{D.}$ $2 \sqrt{5} \mathrm{~cm}$
一次函数 $y=-3 x-1$ 的图象过点 $\left(x_1, y_1\right),\left(x_1+1, y_2\right),\left(x_1+2, y_3\right)$, 则 $y_1, y_2, y_3$ 的大小关系 为
$\text{A.}$ $y_1 < y_2 < y_3$
$\text{B.}$ $y_3 < y_2 < y_1$
$\text{C.}$ $y_2 < y_1 < y_3$
$\text{D.}$ $3 < y_1 < y_2$
本学期, 我们学习了用赵爽弦图证明勾股定理. 在如图所示的赵爽弦图中, 在 $D H$ 上取点 $M$ 使得 $D M=G H$, 连接 $A M 、 C M$. 若正方形 $E F G H$ 的面积为 6, 则 $\triangle A D M$ 与 $\triangle C D M$ 的面积之差为
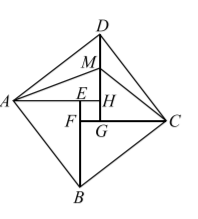
$\text{A.}$ 3
$\text{B.}$ 2
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ 不确定
如图, 在平面直角坐标系中, 线段 $A B$ 的端点为 $A(-3,1), B(1,2)$, 若直线 $y=k x-1$ 与线段 $A B$ 有交点, 则 $k$ 的值不能是
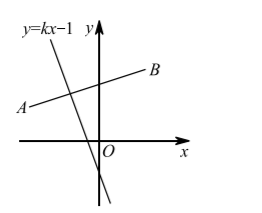
$\text{A.}$ 2
$\text{B.}$ 4
$\text{C.}$ -2
$\text{D.}$ -4
填空题 (共 5 题 ),请把答案直接填写在答题纸上
若 $\sqrt{x-6}$ 在实数范围内有意义, 请写出 $x$ 的取值范围
函数 $y=m x-1$ 的图象经过 $(1,3)$, 则 $m=$
在平面直角坐标系中, 点 $A(-2,1), B(2,4), C(x, y), B C / / y$ 轴, 当线段 $A C$ 最短时, 则 此时 $\triangle A B C$ 的面积为
如图是一个供滑板爱好者使用的 $U$ 型池, 该 $U$ 型池可以看作是一个长方体去掉一个半圆柱而成, 中间可供滑行部分的截面是半径为 $4 \mathrm{~m}$ 的半圆, 其边缘 $A B=C D=20 \mathrm{~m}$, 点 $E$ 在 $C D$ 上, $C E=4 \mathrm{~m}$, 一滑行爱好者从 $A$ 点滑行到 $E$ 点, 则他滑行的最短距离为 ( ) $\mathrm{m}(\pi$ 的值为 3$)$.

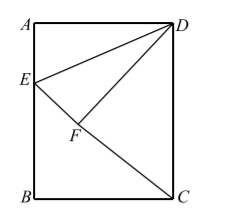
如图, 长方形 $A B C D$ 中, 点 $E$ 是边 $A B$ 上一点, 连接 $D E$, 将 $\triangle A D E$ 沿 $D E$ 翻折, 点 $A$ 落在点 $F$ 处, 连接 $C F, A B=10, B C=8$, 若 $\triangle D F C$ 是等腰三角形, 则 $A E=$
解答题 (共 7 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算:
(1) $\sqrt{18}+|2-\sqrt{2}|-(\pi+2021)^0$;
(2) $(3+\sqrt{2})^2+(1+\sqrt{2})(1-\sqrt{2})$.
如图, 在平面直角坐标系中, $\triangle A B C$ 的位置如图所示(每个方格的边长均为 1 个单位长 度).
(1) 写出下列点的坐标: $A,B,C$
(2) 若 $\triangle A B C$ 各顶点的纵坐标不变, 横坐标都乘 -1, 请在同一平面直角坐标系中找出对应的点 $A^{\prime}$, $B^{\prime}, C^{\prime}$, 并依次连接这三个点, 从图象可知 $\triangle A B C$ 与 $\triangle A^{\prime} B^{\prime} C^{\prime}$ 有怎样的位置关系?
(3) 请在 $x$ 轴上作出一点 $P$, 使得 $P B+P C$ 最小. 注意: 将点 $P$ 标出, 保留作图痕迹.
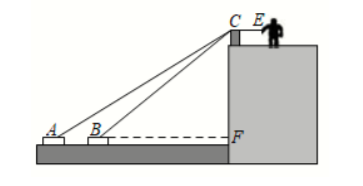
如图, 在一条绷紧的绳索一端系着一艘小船. 河岸上一男孩挭着绳子另一端向右走, 绳端 从 $C$ 移动到 $E$, 同时小船从 $A$ 移动到 $B$, 且绳长始终保持不变. 回答下列问题:
(1) 根据题意可知: $A C$ ( ) $B C+C E$ ( 填 >、 < 、= ).
(2) 若 $C F=5$ 米, $A F=12$ 米, $A B=9$ 米,求小男孩需向右移动的距离. (结果保留根号)
先阅读, 后解答:
(1) 由根式的性质计算下列式子得:
(1) $\sqrt{3^2}=3$, (2) $\sqrt{\left(\frac{2}{3}\right)^2}=\frac{2}{3}$, (3) $\sqrt{\left(-\frac{1}{3}\right)^2}=\frac{1}{3}$, (4) $\sqrt{(-5)^2}=5$, (5) $\sqrt{0}=0$.
由上述计算, 请写出 $\sqrt{a^2}$ 的结果 ( $a$ 为任意实数).
(2) 利用 (1) 中的结论, 直接写出下列问题的结果:
(1) $\sqrt{(3.14-\pi)^2}=$
(2)化简: $\sqrt{x^2-4 x+4}(x < 2)=$
(3) 应用:
若 $\sqrt{(x-5)^2}+\sqrt{(x-8)^2}=3$, 求满足条件的所有整数 $x$ 的和
“十一”黄金周, 贝塔一家随团到某风景区旅游, 集体门票的收费标准是: 25 人以内(含 25 人,每人 30 元;超过 25 人的, 超过部分每人 10 元.
(1)写出应收门票费 $y$ (元)与游览人数 $x$ (人)之间的关系式;
(2)若贝塔一家所在的旅游团购门票花了 1050 元, 则该旅游团共有多少人?
在一次函数学习中, 我们经历了列表、描点、连线画函数图象, 结合图象研究函数性质并 对其性质进行应用的过程. 小华根据学习函数的经验, 对函数 $y=|x|-2$ 的图象与性质进行了探 究. 请同学们阅读探究过程并解答:
在函数 $y=|x|-2$ 中, 自变量 $x$ 可以是任意实数.
(1) 下表是 $y$ 与 $x$ 的几组对应值:

m=,n=
(2)在平面直角坐标系 $x O y$ 中, 描出表中各组对应值为坐标的点. 并根据描出的点, 画出该函数 的图象;
根据函数图象可得:
(1) 当 $x=$ 时, $y$ 有最小值为
(2)请写出该函数的一条性质;
(3)如果 $y=|x|-2$ 的图象与直线 $y=k$ 有两个交点, 则 $k$ 的取值范围是
如图 1, 对角线互相垂直的四边形叫做垂直四边形.
(1) 概念理解: 如图 2, 在四边形 $A B C D$ 中, $A B=A D, B C=C D$, 问四边形 $A B C D$ 是垂直四边 形吗?请说明理由;
(2) 性质探究: 如图 1, 垂直四边形 $A B C D$ 的对角线 $A C, B D$ 交于点 $O$. 猜想: $A B^2+C D^2$ 与 $A D^2+B C^2$ 有什么关系? 并证明你的猜想.
(3) 解决问题: 如图 3, 分别以 Rt $\triangle A C B$ 的直角边 $A C$ 和斜边 $A B$ 为边向外作正方形 $A C F G$ 和正方 形 $A B D E$, 连接 $C E, B G, G E$. 已知 $A C=2, A B=3$, 求 $G E$ 的长.
