单选题 (共 10 题 ),每题只有一个选项正确
已知向量 $\vec{a}, \vec{b}$ 满足 $|\vec{b}|=2, \vec{a}$ 与 $\vec{b}$ 的夹角为 $60^{\circ}$, 则当实数 $\lambda$ 变化时, $|\vec{b}-\lambda \vec{a}|$ 的最小值为
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $2$
$\text{C.}$ $\sqrt{10}$
$\text{D.}$ $2 \sqrt{3}$
已知 $\triangle A B C$ 为等边三角形, $A B=2$, 设点 $P 、 Q$ 满足 $\overrightarrow{A P}=\lambda \overrightarrow{A B}, \overrightarrow{A Q}=(1-\lambda) \overrightarrow{A C}, \lambda \in R$, 若 $\overrightarrow{B Q} \cdot \overrightarrow{C P}=-\frac{3}{2}$, 则 $\lambda=$
$\text{A.}$ $\frac{1}{8}$
$\text{B.}$ $\frac{1}{4}$
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ $\frac{3}{4}$
已知 $\triangle A B C$ 的外接圆圆心为 $O$, 且 $2 \overrightarrow{A O}=\overrightarrow{A B}+\overrightarrow{A C},|\overrightarrow{O A}|=|\overrightarrow{A B}|$, 则向量 $\overrightarrow{O C}$ 在向量 $\overline{C A}$ 上的投影向量为
$\text{A.}$ $\frac{1}{2} \overrightarrow{C A}$
$\text{B.}$ $\frac{\sqrt{3}}{2} \overrightarrow{O C}$
$\text{C.}$ $-\frac{1}{2} \overrightarrow{C A}$
$\text{D.}$ $-\frac{\sqrt{3}}{2} \overrightarrow{O C}$
已知 $P$ 是等边三角形 $A B C$ 所在平面内一点, 且 $A B=2 \sqrt{3}, B P=1$, 则 $\overrightarrow{A P} \cdot \overrightarrow{C P}$ 的最 小值是
$\text{A.}$ $1$
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $2$
已知单位向量 $\vec{a}$ 与向量 $\vec{b}=(0,2)$ 垂直, 若向量 $\vec{c}$ 满足 $|\vec{a}+\vec{b}+\vec{c}|=1$, 则 $|\vec{c}|$ 的取值范围 为
$\text{A.}$ $[1, \sqrt{5}-1]$
$\text{B.}$ $\left[\frac{\sqrt{3}-1}{2}, \frac{\sqrt{3}+1}{2}\right]$
$\text{C.}$ $[\sqrt{5}-1, \sqrt{5}+1]$
$\text{D.}$ $\left[\frac{\sqrt{3}+1}{2}, 3\right]$
已知向量 $\vec{a}, \vec{b}$ 满足 $\vec{a}=(\sqrt{3}, 1), \vec{a} \cdot \vec{b}=4$, 则 $|\vec{b}|$ 的最小值为
$\text{A.}$ 1
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ 3
在平行四边形 $A B C D$ 中, $E, F$ 分别是 $B C, C D$ 的中点, $D E$ 交 $A F$ 点 $G$, 则 $\overrightarrow{A G}=$

$\text{A.}$ $\frac{2}{5} \overrightarrow{A B}-\frac{4}{5} \overrightarrow{B C}$
$\text{B.}$ $\frac{2}{5} \overrightarrow{A B}+\frac{4}{5} \overrightarrow{B C}$
$\text{C.}$ $-\frac{2}{5} \overrightarrow{A B}+\frac{4}{5} \overrightarrow{B C}$
$\text{D.}$ $-\frac{2}{5} \overrightarrow{A B}-\overrightarrow{B C}$
已知点 $O$ 为 $\triangle A B C$ 所在平面内的一点, 且 $\overrightarrow{O A}^2=\overrightarrow{O B}^2=\overrightarrow{O C}^2, \overrightarrow{O A} \cdot \overrightarrow{O B}=\overrightarrow{O B} \cdot \overrightarrow{O C}=\overrightarrow{O C}$. $\overrightarrow{O A}=-2$, 则 $\triangle A B C$ 的面积为
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ $3 \sqrt{3}$
$\text{D.}$ $\frac{5 \sqrt{3}}{4}$
在 $\triangle A B C$ 中, $\overrightarrow{A B} \cdot \overrightarrow{A C}=9, \sin (A+C)=\cos A \sin C, S_{\triangle A B C}=6, P$ 为线段 $A B$ 上的动 点, 且 $\overrightarrow{C P}=x \cdot \frac{\overrightarrow{C A}}{|\overrightarrow{C A}|}+y \cdot \frac{\overrightarrow{C B}}{|\overrightarrow{C B}|}$, 则 $\frac{2}{x}+\frac{1}{y}$ 的最小值为
$\text{A.}$ $\frac{11}{6}+\frac{\sqrt{6}}{3}$
$\text{B.}$ $\frac{11}{6}$
$\text{C.}$ $\frac{11}{12}+\frac{\sqrt{6}}{3}$
$\text{D.}$ $\frac{11}{12}$
$\triangle A B C$ 中, $A C=\sqrt{2}, A B=2, A=45^{\circ}, P$ 是 $\triangle A B C$ 外接圆上一点, $\overrightarrow{A P}=\lambda \overrightarrow{A B}+\mu \overrightarrow{A C}$, 则 $\lambda+\mu$ 的最大值是
$\text{A.}$ $\frac{\sqrt{2}+1}{2}$
$\text{B.}$ $\frac{\sqrt{2}-1}{2}$
$\text{C.}$ $\frac{\sqrt{3}-\sqrt{2}}{2}$
$\text{D.}$ $\frac{\sqrt{3}+\sqrt{2}}{2}$
多选题 (共 5 题 ),每题有多个选项正确
已知复数 $z_1$ 对应的向量为 $\overrightarrow{O Z_1}$, 复数 $z_2$ 对应的向量为 $\overrightarrow{O Z_2}$, 则
$\text{A.}$ 若 $\left|z_1+z_2\right|=\left|z_1-z_2\right|$, 则 $\overline{O Z_1} \perp \overline{O Z_2}$
$\text{B.}$ 若 $\left(\overrightarrow{O Z_1}+\overrightarrow{O Z_2}\right) \perp\left(\overrightarrow{O Z_1}-\overrightarrow{O Z_2}\right)$, 则 $\left|z_1\right|=\left|z_2\right|$
$\text{C.}$ 若 $z_1$ 与 $z_2$ 在复平面上对应的点关于实轴对称, 则 $z_1 z_2=\left|z_1 z_2\right|$
$\text{D.}$ 若 $\left|z_1\right|=\left|z_2\right|$, 则 $z_1^2=z_2^2$
已知 $\triangle A B C$ 是半径为 2 的圆 $O$ 的内接三角形, 则下列说法正确的是
$\text{A.}$ 若角 $C=\frac{\pi}{3}$, 则 $\overrightarrow{A B} \cdot \overrightarrow{A O}=12$
$\text{B.}$ 若 $2 \overrightarrow{O A}+\overrightarrow{A B}+\overrightarrow{A C}=\overrightarrow{0}$, 则 $|\overrightarrow{B C}|=4$
$\text{C.}$ 若 $|\overrightarrow{O A}-\overrightarrow{O B}|=\overrightarrow{O A} \cdot \overrightarrow{O B}$, 则 $\overrightarrow{O A}, \overrightarrow{O B}$ 的夹角为 $\frac{\pi}{3}$
$\text{D.}$ 若 $(\overrightarrow{B C}+\overrightarrow{B A}) \cdot \overrightarrow{A C}=|\overrightarrow{A C}|^2$, 则 $A B$ 为圆 $O$ 的一条直径
中华人民共和国的国旗图案是由五颗五角星组成, 这些五角星的位置关系象征着中 国共产党领导下的革命与人民大团结. 如图, 五角星是由五个全等且顶角为 $36^{\circ}$ 的等腰 三角形和一个正五边形组成. 已知当 $A B=2$ 时, $B D=\sqrt{5}-1$, 则下列结论正确的为
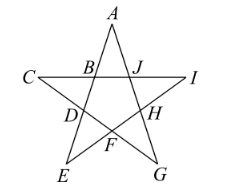
$\text{A.}$ $|\overrightarrow{D E}|=|\overrightarrow{D H}|$
$\text{B.}$ $\overrightarrow{A F} \cdot \overrightarrow{B J}=0$
$\text{C.}$ $\overrightarrow{A H}=\frac{\sqrt{5}+1}{2} \overrightarrow{A B}$
$\text{D.}$ $\overrightarrow{C B}+\overrightarrow{C D}=\overrightarrow{J C}-\overrightarrow{J H}$
已知 $\triangle A B C$ 中, $A B=3, A C=5, B C=7, O$ 为 $\triangle A B C$ 外接圆的圆心, $I$ 为 $\triangle A B C$ 内切 圆的圆心,则下列叙述正确的是
$\text{A.}$ $\triangle A B C$ 外接圆半径为 $\frac{14 \sqrt{3}}{3}$
$\text{B.}$ $\triangle A B C$ 内切圆半径为 $\frac{\sqrt{3}}{2}$
$\text{C.}$ $\overrightarrow{A O} \cdot \overrightarrow{B C}=8$
$\text{D.}$ $\overrightarrow{A I} \cdot \overrightarrow{B C}=1$
定义平面向量的一种运算“ $\Theta$ ”如下:对任意的两个向量 $\vec{a}=\left(x_1, y_1\right), \vec{b}=\left(x_2, y_2\right)$, 今 $\vec{a} \Theta \vec{b}=\left(x_1 y_2-x_2 y_1, x_1 x_2+y_1 y_2\right)$, 下面说法一定正确的是
$\text{A.}$ 对任意的 $\lambda \in R$, 有 $(\lambda \vec{a}) \Theta \vec{b}=\lambda(\vec{a} \Theta \vec{b})$
$\text{B.}$ 存在唯一确定的向量 $\vec{e}$ 使得对于任意向量 $\vec{a}$, 都有 $\vec{a} \Theta \vec{e}=\vec{e} \Theta \vec{a}=\vec{a}$ 成立
$\text{C.}$ 若 $\vec{a}$ 与 $\vec{b}$ 垂直, 则 $(\vec{a} \Theta \vec{b}) \Theta \vec{c}$ 与 $\vec{a} \Theta(\vec{b} \Theta \vec{c})$ 共线
$\text{D.}$ 若 $\vec{a}$ 与 $\vec{b}$ 共线, 则 $(\vec{a} \Theta \vec{b}) \Theta \vec{c}$ 与 $\vec{a} \Theta(\vec{b} \Theta \vec{c})$ 的模相等
填空题 (共 10 题 ),请把答案直接填写在答题纸上
在平面直角坐标系 $x O y$ 中, $r>0, \odot M:(x-r)^2+y^2=\frac{3 r^2}{4}$ 与抛物线 $C: y^2=4 x$
有且仅有两个公共点, 直线 $l$ 过圆心 $M$ 且交抛物线 $C$ 于 $A, B$ 两点, 则 $\overrightarrow{O A} \cdot \overrightarrow{O B}=$
已知 $\triangle A B C$ 是等边三角形, $E, F$ 分别是 $A B$ 和 $A C$ 的中点, $P$ 是 $\triangle A B C$ 边上一动点, 则 满足 $\overrightarrow{P E} \cdot \overrightarrow{P F}=\overrightarrow{B E} \cdot \overrightarrow{C F}$ 的点 $P$ 的个数为
已知平面向量 $\overrightarrow{e_1}, \overrightarrow{e_2}$ 满足 $\left|2 \overrightarrow{e_2}-\overrightarrow{e_1}\right|=2$, 设 $\vec{a}=\overrightarrow{e_1}+4 \overrightarrow{e_2}, \vec{b}=\overrightarrow{e_1}+\overrightarrow{e_2}$, 若 $1 \leq \vec{a} \cdot \vec{b} \leq 2$, 则 $|\vec{a}|$ 的取值范围为
已知 $\triangle A B C$ 的内角 $A, B, C$ 所对的边分别为 $a, b, c, A=\frac{\pi}{3}, c=3, a \sin B=\sqrt{3}, D, E$ 分 别为线段 $A B, A C$ 上的动点, $\frac{A D}{A B}=\frac{C E}{C A}$, 则 $D E$ 的最小值为
在平行四边形 $A B C D$ 中, $|\overrightarrow{A B}+\overrightarrow{A D}|=|B \overrightarrow{B D}|=3,|\overrightarrow{A B}|=1$, 则 $\overrightarrow{A C} \cdot \overrightarrow{B D}=$
已知非零向量 $\vec{a}, \vec{b}$ 满足 $|\vec{a}|=|\vec{b}|$, 且 $(\vec{a}+\vec{b}) \perp \vec{b}$, 则 $\vec{a}$ 与 $\vec{b}$ 的夹角为
已知半径为 1 的圆 $O$ 上有三个动点 $A, B, C$, 且 $|A B|=\sqrt{2}$, 则 $\overrightarrow{A C} \cdot \overrightarrow{B C}$ 的最小值为
已知菱形 $A B C D$ 的边长为 $2, \angle B A D=120^{\circ}$, 点 $E, F$ 分在边 $B C, C D$ 上, $\overrightarrow{B E}=\lambda \overrightarrow{B C}$, $D F=\mu D C$. 若 $\lambda+\mu=\frac{2}{3}$, 则 $\overrightarrow{A E} \cdot \overrightarrow{A F}$ 的最小值为
设 $\vec{a}, \vec{b}$ 为不共线的向量, 满足 $\vec{c}=\lambda \vec{a}+\mu \vec{b}, 3 \lambda+4 \mu=2(\lambda, \mu \in \mathrm{R})$, 且 $|\vec{c}|=|\vec{a}-\vec{c}|=$ $|\vec{b}-\vec{c}|$, 若 $|\vec{a}-\vec{b}|=3$, 则 $(|\vec{a}| \cdot|\vec{b}|)^2-(\vec{a} \cdot \vec{b})^2$ 的最大值为
已知平面向量 $\vec{a}, \vec{b}, \vec{c}$ 满足 $|\vec{a}|=1,|\vec{b}|=|\vec{c}|=2 \sqrt{2}$, 且 $(\vec{a}-\vec{b}) \cdot(\vec{a}-\vec{c})=0, \theta=$ $\langle\vec{a}, \vec{b}\rangle\left(0 \leq \theta \leq \frac{\pi}{4}\right)$, 则 $\frac{\vec{b} \cdot(\vec{a}-\vec{c})}{|\vec{a}-\vec{c}|}$ 的取值范围是