单选题 (共 6 题 ),每题只有一个选项正确
设 $P(A B)=0$, 则必有 $(\quad)$ 。
$\text{A.}$ 事件 $A, B$ 互不相容
$\text{B.}$ 事件 $A, B$ 互为对立事件
$\text{C.}$ $P(A B)=P(A) P(B)$
$\text{D.}$ $P(A-B)=P(A)$
设 $F(x)$ 是某随机变量的分布函数,则以下函数一定是分布函数的是
$\text{A.}$ $F(-x)$
$\text{B.}$ $F(0.3 x)$
$\text{C.}$ $F\left(x^{-1}\right)$
$\text{D.}$ $F\left(x^2\right)$
设随机变量 $X, Y$ 不相关, 则一定有
$\text{A.}$ $X, Y$ 的协方差等于 0
$\text{B.}$ $X, Y$ 相互独立
$\text{C.}$ $D(X-Y)=D(X)-D(Y)$
$\text{D.}$ $D(X Y)=D(X) D(Y)$
设 $X_1, \cdots, X_n$ 是简单随机样本, 来自总体 $X \sim N\left(\mu, \sigma^2\right)$, 其中 $\mu, \sigma$ 是未知参数, 则以下是统计量的是()。
$\text{A.}$ $X_1+X_2+\cdots+X_n-n^2 E(\bar{X})$
$\text{B.}$ $X_1+X_2+\cdots+X_n-n \mu$
$\text{C.}$ $\frac{X_1+X_2+\cdots+X_n}{n \sqrt{S^2}}$
$\text{D.}$ $\frac{X_1+X_2+\cdots+X_n}{n \sigma}$
设总体 $X$ 服从参数为 $\lambda$ 的泊松分布, 简单样本 $X_1, X_2, \cdots, X_n$ 来自该总体, $\bar{X}, S^2$ 分别是样本均值和样本方差,则以下不能作为未知参数 $\lambda$ 的矩估计量的是
$\text{A.}$ $\bar{X}$
$\text{B.}$ $S^2$
$\text{C.}$ $S$
$\text{D.}$ $\frac{-1+\sqrt{1+\frac{4}{n} \sum_{i=1}^n X_i^2}}{2}$
设简单样本 $X_1, \cdots, X_n$ 来自标准正态分布, $\bar{X}, S^2$ 分别是样本均值和样本方差, 则以下选项正确的是()。
$\text{A.}$ $\bar{X} \sim N(0,1)$
$\text{B.}$ $\bar{X}^2$ 服从卡方分布
$\text{C.}$ $S^2$ 服从卡方分布
$\text{D.}$ $\frac{n \bar{X}^2}{S^2}$ 服从 $F$ 分布
填空题 (共 6 题 ),请把答案直接填写在答题纸上
若 $X$ 服从区间 $[0,5]$ 上的均匀分布, 则 $E\left(e^{-X}\right)=$
设 $X, Y$ 相互独立, $X$ 的分布律为 $P\{X=1\}=0.2, P\{X=2\}=0.8, Y \sim U(0,5)$,则 $P\{X+Y \leqslant 3\}=$
若 $X \sim t(n)$, 且 $P\left\{X^2>4\right\}=0.3$, 则 $P\{X>-2\}=$
若随机变量 $X$ 服从参数为 3 的指数分布, 即它具有概率密度函数 $f(x)=$ $3 e^{-3 x}(x \geqslant 0)$, 定义 $P\left\{X>z_\alpha\right\}=\alpha$, 求 $z_{0.5}=$
设 $(X, Y) \sim N(2,1,4,9,-0.5)$, 则 $X$ 与 $Y$ 的协方差等于
设 $Y \sim B(n, 0.5)$, 要使得 $P\{Y \leqslant 40\} \leqslant 0.98$, 则 $n$ 的最小值约为 $\qquad$。 (标准正态分布表: $\Phi(2)=0.98, \Phi(-2)=0.02$ )
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设 $(X, Y)$ 具有概率密度函数 $f(x, y)=\left\{\begin{array}{ll}a x y, & 0 < y \leqslant x < 1 ; \\ 0, & \text { 其他. }\end{array}\right.$ 其中 $a$ 是常数. (1) 求常数 $a$ 的值; (2) 计算概率 $P\left\{Y>X^2\right\}$; (3) 当 $0 < y < 1$ 时, 求条件概率密度函数 $f_{X \mid Y}(x \mid y)$.
设随机变量$X,Y$的分布分布为
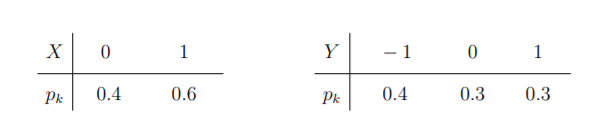
且 $P\{X \neq Y\}=1$. (1) 求 $X, Y$ 的联合分布律; (2) 协方差 $\operatorname{cov}(X, X Y)$
设总体 $X$ 具有概率密度函数 $f(x ; \alpha)=\left\{\begin{array}{ll}\frac{\alpha}{1-\alpha} x^{\frac{\alpha}{1-\alpha}-1}, & 0 < x < 1 \\ 0, & \text { 其他 }\end{array}\right.$ 其中 $0 < \alpha < 1$ 是未知参数, $X_1, X_2, \cdots, X_n$ 是来自该总体的一个简单样本. (1) 求 $\alpha$ 的矩估计量 $\hat{\alpha}_1$ ;(2)求 $\alpha$ 的最大似然估计量 $\hat{\alpha}_2$ ;(3)令 $\hat{\alpha}_3=\max \left\{X_1, X_2, \cdots, X_n\right\}$ ,求 $E\left(\hat{\alpha}_3\right)$.
在针织品漂白工艺过程中, 需要考察温度对针织品断裂强度的影响。假设在 80 摄氏度时, 针织品的断裂强度服从正态分布 $N\left(\mu, \sigma^2\right)$, 现获得来自该总体的一个简单样本 $X_1, X_2, \cdots, X_n$, 其样本值为: $1.3,1.2,1.2,1.5,1.1$
(1) 求 $\mu$ 的置信水平为 0.9 的置信区间; (2) 如果 $\sigma=0.5$ 时, 认为该批次针织品的断裂强度是稳定的, 在显著性水平为 0.05 时, 通过该样本值判断针织品的断裂强度是否稳定.
$\left(\right.$ 上分位数表 $t_{0.05}(4)=2.13, t_{0.05}(5)=2.01, \chi_{0.05}^2(4)=9.5, \chi_{0.95}^2(4)=0.7, \chi_{0.025}^2(4)=$ $\left.11.1, \chi_{0.975}^2(4)=0.5\right)$ 。